ベクトル空間の基底が変換されたときに、対応する双対基底の変換行列が元の変換行列の転置行列の逆行列になることを示す。テンソルの半変ベクトルや共変ベクトルにもつながる。

1. 双対空間の基底変換

まず、ベクトル空間に対して、双対空間というものが定まる。
これは、ベクトル空間は、向きや強さを表すものですが、対応する双対空間は、センサーのようなものと自分は理解しています。つまり、ベクトルに対して、あるスカラーを返す関数が双対空間です。

物理現象を調べるときに、向きや大きさと見るか、それを測るセンサーで見るか、問題に応じて設定を変えることが重要と認識しています。これに関しては、まだまだ物理やテンソルの理解ができておらず、今後考えをまとめられればと思っています。

さて、ベクトル空間 \( V \) の基底を \( \langle v_1, \dots, v_n \rangle \)として、新しい基底を \( \langle v_1′, \dots, v_n’ \rangle \) とします。

ベクトルはどのような観測者（基底）から見ても、同じものを指し示すはずです。観測者が異なると、成分の表示が変わります。この変換は以下のようになります。

\[
(v_1′, \dots, v_n’) = (v_1, \dots, v_n) P
\quad\text{ただし } P = (p_{ij})
\]
実際、このように変換行列により基底変換される。

ベクトル空間の基底変換

さて、このとき、双対空間 \( V^* \) の基底を \( \langle \phi^1, \dots, \phi^n \rangle \)、
新しい基底を \( \langle \phi’^1, \dots, \phi’^n \rangle \) とし、同様に以下のように変換するとする。

\[
(\phi’^1, \dots, \phi’^n) = (\phi^1, \dots, \phi^n) Q
\quad\text{ただし } Q = (q_{ij})
\]

このとき、双対空間の変換行列 \( Q \)と、もとのベクトル空間の変換行列\( P \)との関係を調べたい。

まず、双対空間の基底は、以下の記事のようになる。

双対空間の基底

つまり、
\[
\phi^i(v_j) = \delta^i_j
\quad\text{（旧基底）}, \quad
\phi’^i(v_j’) = \delta^i_j
\quad\text{（新基底）}
\]

このような条件のもと、双対基底の基底変換がどうなるか計算する。

条件より、
\[
\phi’^i(v_j’)
= \left( \sum_k q_{ki} \phi^k \right)
\left( \sum_\ell p_{\ell j} v_\ell \right)
= \sum_{k, \ell} q_{ki} p_{\ell j} \phi^k(v_\ell)
\]

\[
= \sum_{k, \ell} q_{ki} p_{\ell j} \delta^k_\ell
= \sum_k q_{ki} p_{k j}
\]

この結果が \( \delta^i_j \) である必要があるので、

\[
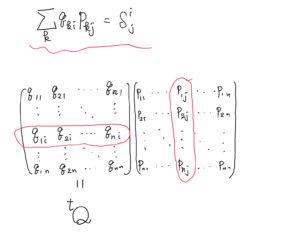
\sum_k q_{ki} p_{k j} = \delta^i_j
\quad\text{すなわち}\quad
Q^{\mathrm{T}} P = I
\quad\Rightarrow\quad
Q = (P^{\mathrm{T}})^{-1}
\]

—

2. 結果

よって、双対空間の基底の変換行列 \( Q \) は、ベクトル空間の基底変換行列 \( P \) の **転置の逆行列**になります：

\[
Q = (P^{\mathrm{T}})^{-1}
\]

この関係により、双対空間の基底は「ベクトル空間の基底変換に共変」し、その成分は「反変」なベクトルの変換法則とは逆に、**変換行列そのもので変換される**ことがわかります。
これに関しては別でまとめます。

==================================

クリックで応援よろしくお願いします.

にほんブログ村