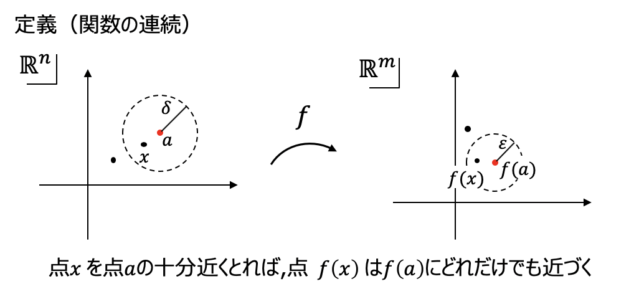
解析学を学ぶ上で基本的かつ重要な概念に「関数の連続」があります.
二次関数のグラフは本当に繋がっているのか?どうやって証明する?
例題を解きながらその証明方法を理解していきます.
月: 2019年10月
マスパーティに参加してきました
今回,2019年10月19〜20日に横浜で開催された数学イベント「マスパーティ」に参加してきましたので,そのレポートをさせていただこうと思います.
時間の都合上,一部にしか参加することはできませんでしたが,趣味で数学をされている方の熱い思いを感じることができました.
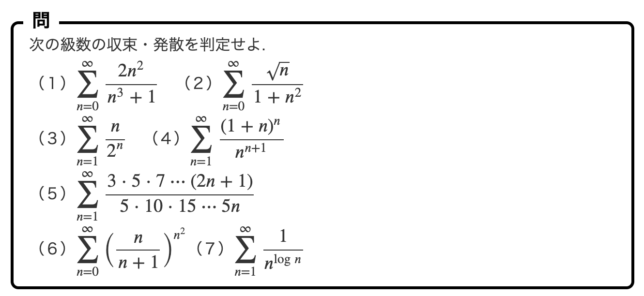
例題で理解する級数の収束・発散判定(解析学 第I章 実数と連続10)
加藤文元「宇宙と宇宙をつなぐ数学」教養としての数学者の発想
IUT理論とはInter Universal Teichmüller理論=宇宙際(うちゅうさい)タイヒミュラー理論のことで,京都大学望月教授が2012年8月30日に発表し数学会に衝撃を与えている理論です.
加藤文元教授による著書「宇宙と宇宙をつなぐ数学 IUT理論の衝撃」では,IUT理論の雰囲気が分かりやすく紹介がされています.
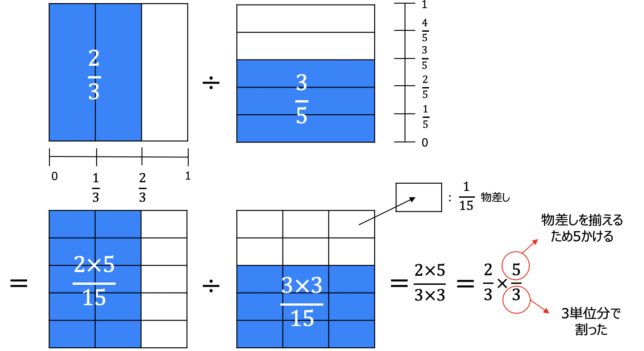
何で分数の割り算は逆数をかけるの?理由を説明できますか?
もし子供に「何で分数の割り算は逆数をかけるの?」と聞かれたら,何と答えますか?
小学校で分数の割り算の仕方は習いましたが,何でそうなのかと改めて考えると結構難しいものです.
今回は割り算に関して,その本質に迫り,上記質問の回答を考えたいと思います.
子供への数学教育としてどうぞ.
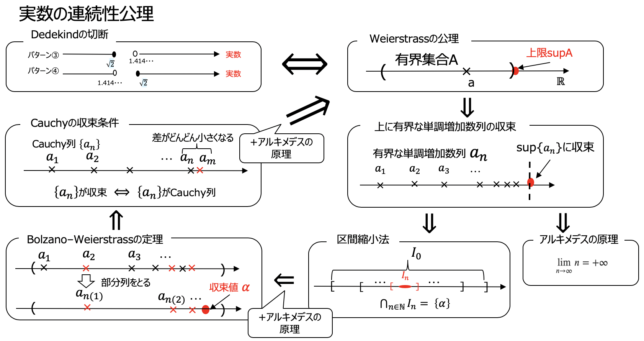
6つの同値な「実数の連続性公理」まとめ(解析学 第I章 実数と連続9)
これまで実数の連続性を公理とし,数列の極限について定義,それから導かれる様々な命題,定理を証明してきました.
その結果分かった実数の連続性公理と同値な条件(Bolzano–Weierstrass,Cauhy列の収束+アルキメデスの原理etc)
をまとめたいと思います.
どれを公理としてもよく,自分にあったものを議論の出発点としてよいのです.
コーシーの収束条件から実数の連続性を証明(解析学 第I章 実数と連続8)
我々は今,実数の連続性を公理とし,数列の極限について定義,様々な極限操作を論理的に厳密に扱えるようになりました.
そして,数列の収束を判定するCauchyの収束判定条件を証明しました.
実は,アルキメデスの原理を加えれば,これははじめに仮定した「実数の連続性公理」と同値なのです.
今回はこれを証明します.