ベクトル空間の基底が変換されたときに、対応する双対基底の変換行列が元の変換行列の転置行列の逆行列になることを示す。テンソルの半変ベクトルや共変ベクトルにもつながる。
投稿者: yuyu
2011年に数学科修士を修了.専攻は整数論.現在は数学に関わるような仕事を求めてIT系企業に勤めております.
数学の研究そのものよりも人類の叡智である数学の最先端を追いかけたく,日々数学書を読んでいます.また,数学の美しさ楽しさを自分の言葉でより多くの人に知ってもらいたいという思いも持っています.
線型写像と双線型写像の空間の基底
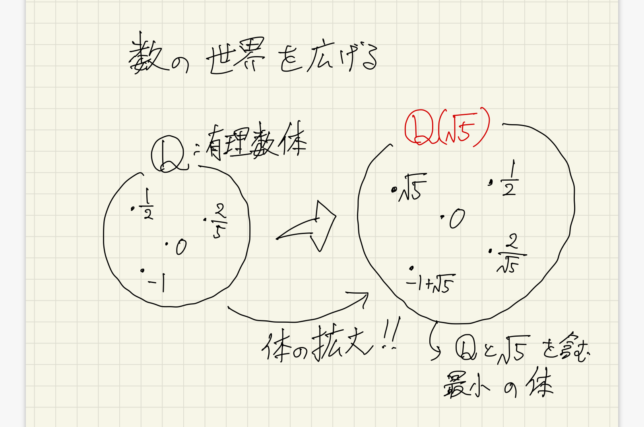
ベクトル空間の基底変換
双対空間の基底
ガロア理論その1 〜解の公式が作れるということ〜
長年の夢だった「ガロア理論」についてまとめていく。
ガロア理論は大学の学部数学における一里塚であり、理論の美しさもさることながら、その背景にある歴史、数学者の逸話なども楽しめる。私はこの理論が好きすぎてパリに旅行に行った際に、ガロア所縁の地を旅したほど。
またガロア理論や群という考えは現代数学の基本にもなっている。
いつの日か自分で理解してブログにまとめたいと思っていた。
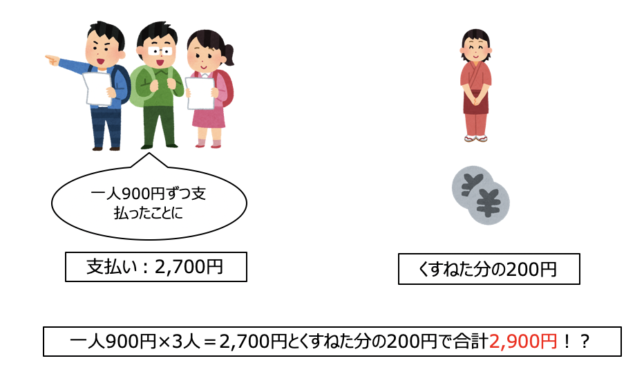
100円はどこに消えた！？
ポアソン分布と指数分布の使いどころ
コンパクトと最大値・最小値の原理（解析学 第I章 実数と連続13）
これまで,点列コンパクト,開集合,閉集合という空間の距離を数学的に表現してきました.
今回はこれら準備してきた概念を用いて,コンパクト空間上の連続関数が最大値・最小値を持つことを証明します.
関数のグラフを描いたり,イメージに頼ったりせず,定義と論理のみで証明できるようになることが数学を学ぶモチベーションであり,数学の素晴らしさなのです.
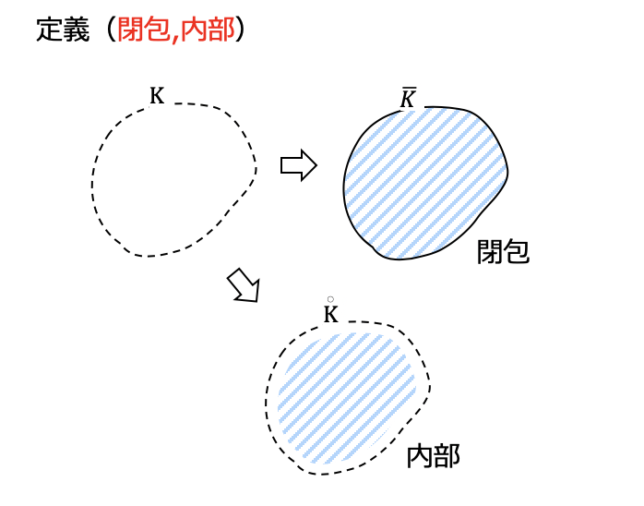
点列コンパクト・開集合・閉集合の整理（解析学 第I章 実数と連続12）
ボルツァーノ・ワイエルシュトラスの定理は,「任意の有界な実数列は収束する部分列を含む」ことを保証しています.これは実数の連続性公理でもあります.
この概念をn次元に一般化したときにも成り立つのか考えます.このような性質を点列コンパクトといいます.
これは開集合や閉集合,コンパクト空間にも繋がる重要な基礎概念です.
これらの概念はたまに教科書を見返したりしていますが,一度整理したいと思います.
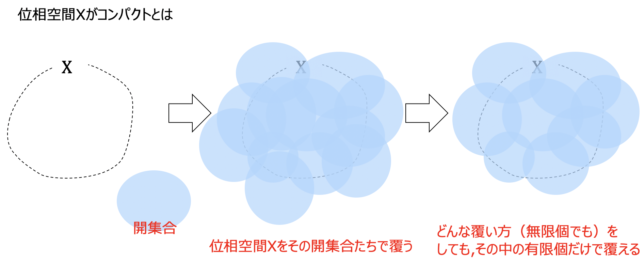
数学におけるコンパクトとは何か
解析や幾何の専門書を読んでいると必ずと言っていいほど現る「コンパクト」という概念.定義だけ見ても何のことやらさっぱりでイメージも掴めない難しい概念です.コンパクトのイメージとその恩恵や考える動機を考えてみます.