ベクトル空間の基底に対して、その基底を変換した際の表現行列や成分の変換について考察する。
目次【本記事の内容】
ベクトル空間の基底変換
ある基底 \( \{e_1, \dots, e_n\} \) で生成されるベクトル空間を\( V = < e_1, \dots, e_n > = < e_i > \)と表す。
この基底 \( <e_1, \dots, e_n> \) を、別の基底 \( <e_1′, \dots, e_n’> \) に変換したとする。
\[
<e_1, \dots, e_n> \longrightarrow <e_1′, \dots, e_n’>
\]
このとき、各\( e_i’ \)を \( \{e_1, \dots, e_n\} \) であらわすと、
\[
e_i’ := a_{i1} e_1 + \cdots + a_{in} e_n
\]
とできるので、それらをならべると、
\[
V = \langle e_1, \ldots, e_n \rangle = \langle e_1′, \ldots, e_n’ \rangle \quad \text{とする。}
\]
\[
\begin{cases}
e_1′ = a_{11}e_1 + a_{12}e_2 + \cdots + a_{1n}e_n \\
e_2′ = a_{21}e_1 + a_{22}e_2 + \cdots + a_{2n}e_n \\
\vdots \\
e_i’ = a_{i1}e_1 + a_{i2}e_2 + \cdots + a_{in}e_n \\
\vdots \\
e_n’ = a_{n1}e_1 + a_{n2}e_2 + \cdots + a_{nn}e_n
\end{cases}
\quad
\]
とできるので、
\[
(e_1′, \ldots, e_n’) = (e_1, \ldots, e_n)
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix} \\
= (e_1, \ldots, e_n)P
\]
🔷 ベクトルの表現と成分の関係
任意のベクトル \( v \in V \) は、旧基底と新基底それぞれで次のように表せるので、
\[
v = (e_1, \dots, e_n)
\begin{pmatrix}
v^1 \\
\vdots \\
v^n
\end{pmatrix} \\
= (e_1′, \dots, e_n’)
\begin{pmatrix}
v^{1′} \\
\vdots \\
v^{n’}
\end{pmatrix}
\]
新基底の定義 \( (e_1′, \dots, e_n’) = (e_1, \dots, e_n) P \) を代入すると：
\[
v = (e_1, \dots, e_n) P
\begin{pmatrix}
v^{1′} \\
\vdots \\
v^{n’}
\end{pmatrix}
\]
よって、両辺を旧基底の係数として比較すると：
\[
\begin{pmatrix}
v^1 \\
\vdots \\
v^n
\end{pmatrix}
= P
\begin{pmatrix}
v^{1′} \\
\vdots \\
v^{n’}
\end{pmatrix}
\quad \Rightarrow \quad
\begin{pmatrix}
v^{1′} \\
\vdots \\
v^{n’}
\end{pmatrix}
= P^{-1}
\begin{pmatrix}
v^1 \\
\vdots \\
v^n
\end{pmatrix}
\]
—
✅ 結論：成分は反変的に変換される
– 基底が変換行列 \( P \) によって変化したとき、
– **ベクトルの成分は \( P^{-1} \) によって変換される。**
つまり、ベクトル成分は**反変的（contravariant）**に振る舞うことがわかる。
この関係はテンソルの変換法則や一般相対性理論における「座標に依らない物理量」の表現において極めて重要となる。
—
—
🔶 アインシュタインの規約を用いて表現する。
あるベクトル \( v \in V \) の成分を、旧基底で \( v^i \)、新基底で \( v^{i’} \) とすると：
\[
v = v^i e_i = v^{i’} e_{i’} = v^{i’} P^j_{i’} e_j
\Rightarrow v^j = P^j_{i’} v^{i’}
\Rightarrow v^{i’} = (P^{-1})^{i’}_j v^j
\]
よって、**ベクトルの成分は逆向き（反変）に変換される。
—
このとき、新しい基底は次のように表される：
\[
e_i’ = P^j_i e_j
\]
ここで \( P \) は**基底変換行列**（新→旧基底）で、添字の上付き・下付きはテンソル的な意味を持つ（共変・反変）。
—
—
==================================
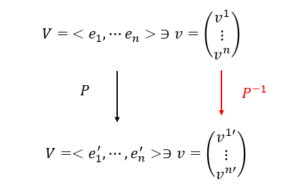
にほんブログ村ランキングに参加しています.クリックで応援よろしくお願いします.
==================================