長年の夢だった「ガロア理論」についてまとめていく。

ガロア理論は大学の学部数学における一里塚であり、理論の美しさもさることながら、その背景にある歴史、数学者の逸話なども楽しめる。私はこの理論が好きすぎてパリに旅行に行った際に、ガロア所縁の地を旅したほど。

またガロア理論や群という考えは現代数学の基本にもなっている。

いつの日か自分で理解してブログにまとめたいと思っていた。

方程式の解の公式が作れるということ

中学校で学んだ二次方程式の解の公式。

これには三次、四次の方程式にも解の公式は存在する。（この方程式は書き下すにはあまりに長すぎるため割愛するが、以前働いていた高校の数学の授業で紹介すると、生徒たちにはウケた。）

三次、四次にも解の公式が存在する。
しかし五次以上の方程式には解の公式は作れない。それは本質的にはクンマーによる巡回拡大が関わっている（と勉強して感じた）。
そしてそれを理解するには、体の拡大と根の置換（群）との関係を学ぶ必要がある。

まずは、中学校で学んだ二次方程式の解の公式を眺めて、解の公式が作れるということを再考する。

二次方程式
$$
ax^{2}+bx+c=0, a,b,c \in \mathbb{Q}
$$

の解の公式は
$$
x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}
$$

例えば、

$$
x^{2}-x-1=0
$$
を公式に沿って解くと、

$$
x=\frac{1\pm \sqrt{1+4}}{2} = \frac{1\pm \sqrt{5}}{2}
$$

この解には、\(\sqrt{5}\)という数が入っており、有理数\(\mathbb{Q}\)の中だけの数の四則演算だけでは解くことができない。

そこで、外の数である\(\sqrt{5}\)を取り入れた四則演算を行う。

つまり、数の世界を広げる。

これが、体の拡大である。

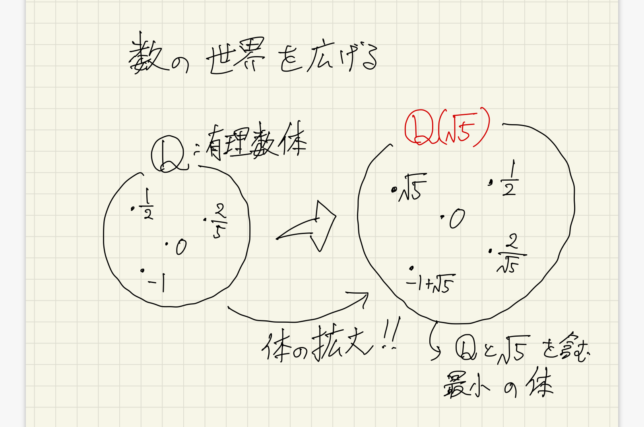
解の公式を作るには、このように外の世界の数を添加し、数の世界を広げる。広げた世界の中の数の四則演算で解を表せばよい。

添加する数は何でもよいわけではなく、元の世界の数の累乗根である必要がある。そうでないと四則演算と” √ “で解けない。そのような適当な数を選べるかどうかが解の公式が作れるかどうかに関わっている。累乗根による数の拡大の様子を調べるのが、クンマーの理論である。

つまり

基礎体の数の累乗根を添加した拡大体が作れる\( \Longleftrightarrow \)ガロア群が巡回群

ガロア理論の本質

そして、どういった数を添加すればよいかを判定するために、ガロア理論がある。ガロア理論では根の置換（シャッフル）を考える。

根のシャッフルによりその数が変化するかどうかで元の世界の数か拡大した世界の数かを判定できる。

• 根の置換により不変な数は、元の世界の数
• 根の置換により変わる数は、拡大した世界の数

根の置換は対称性と関わっており、元の世界の数は対称性が強く置換で不変。

そして、\(\sqrt{}\)を取ることにより対称性が崩れて根の置換で数が変わる。

ガロア理論の本質は根の置換を行うことで根の式の対称性を見出すこと。対称性があれば基礎体の元で、対称性が崩れていれば拡大体の元が判定できる。"√ "を取ることにより、対称性を崩して、代数的に解けるようになる。#ガロア理論 pic.twitter.com/MMWRCtJl93

— ゆうゆう (@yuyu_math) February 18, 2023

対称性を崩していく（√を取る）ことで、数の世界を拡大していき、全ての根が入るような拡大体を元の世界の数の集合（基礎体）から作ることができれば解の公式が作れる。

それを群（根の置換）の世界の言葉で証明していく。

5次以上の方程式には解の公式が作れないことの証明のポイント

① 解の公式が作れる（代数的に解ける）には、

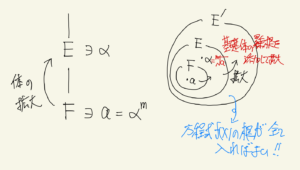
$$
\sqrt[m]{a}=\alpha \in E, \exists a \in F
$$
を基礎体に添加して、体を拡大していき、全ての根が入るような拡大体が作れればよい。

②\(\sqrt[m]{a}=\alpha \)で拡大体\(F(\alpha)\)としたとき、そのガロア群が巡回群になっていれば、元の基礎体から累乗根を付けて拡大できたということ。

どんどん拡大していき、その全てでガロア群が巡回群（ガロア群が可解群）であれば、分解体が体の拡大に含まれる（つまり解の公式が作れる）

③ところが、5次以上の代数方程式では（ガロア群は5次対称群になるが）、可解群になり得ない。つまり、元の基礎体から始めて、分解体が体の拡大に含まれるようにできない。よって、5次以上の方程式に解の公式は作れない。

まとめ

ガロア理論の本質は根の置換を行うことで対称性を見出すこと。またクンマーの理論により体の拡大が元の基礎体から作れるものかどうかが分かる。

体の拡大は数という無限の世界を扱う必要があるが、ガロア理論により、体の拡大は根の置換、つまり群論と対応づけられ、有限の世界を調べることに帰着できる。

次から、体の理論、同型写像の理論の準備をして、その後ガロア理論についてまとめていく。

==================================

クリックで応援よろしくお願いします.

にほんブログ村