ガロア理論は体の拡大について扱っていく。
ここでは体の理論についてまとめる。
体の拡大とは
前回の記事はこちら。解の公式が作れるとはどういうことかを述べました。ガロア理論の準備として体の拡大が重要でした。
Fを体とする。
体とは、単位元を持つ可換環であって、0以外の元がすべて乗法の逆元をもつものとする。
（つまり、四則演算が定義されている集合）
ガロア理論では、数の世界を広げて、どの世界であれば代数的に方程式が解けるのかを考えていく。
数学において、数の世界は、環（かん）や体（たい）という集合で表す。
簡単に言うと、環は、整数のような和、差、積は定義されて、その和差積の答えもその集合に収まっている世界。
体は、環に加えて、商の答えもその世界に収まっているものと思ってもらえればいい。有理数や実数の集合が体である。
そしてガロア理論では、体を考えて数の世界を広げる、つまり体の拡大を考える。
体Fを含むような体Eを考える。
体EはFの拡大体である。
EがFの拡大体であるとき、\(E/F\)のように書く。
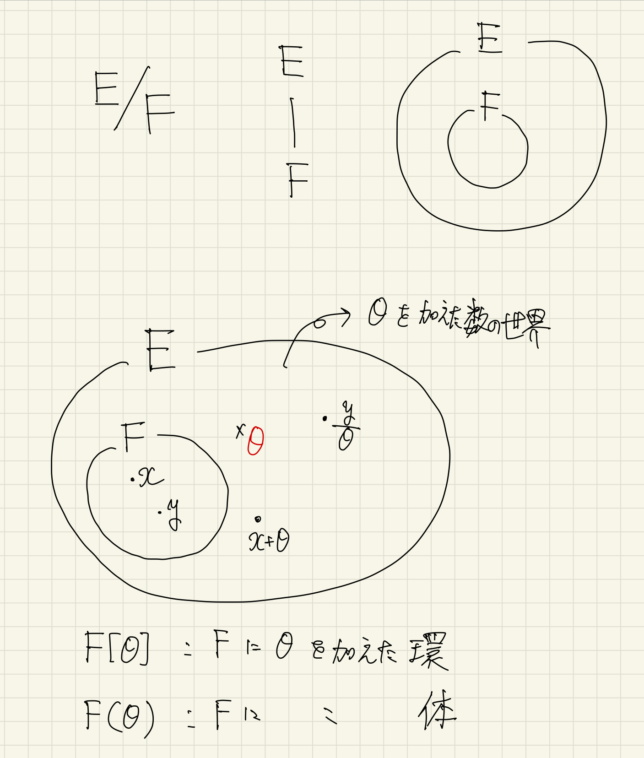
Eは、数の和で閉じており、Fの元をスカラーとみると、EをF上のベクトル空間と見ることができる。
（EはFの元の掛け算をスカラー倍とするベクトル空間の定義を満たす）
ベクトル空間と見るときEのF上の次元を体の拡大次数といい、
$$
[E:F]
$$
で表す。KをEとFの中間の体とする（中間体）と、ベクトル空間の一般論から
$$
[E:F]=[E:K][K:F]
$$
\(\alpha \in E \)が\(F\)上、代数的とは
$$
モニックな多項式 \exists p(x) \in F[X] \quad s.t. \quad p(\alpha)=0
$$
となることをいう。ここに、モニックな多項式とは、多項式の最高次数の係数が1の多項式のこと。
つまり、代数的な数とは、F係数の多項式の方程式の解となる数のことである。
\(\alpha \)が代数的な数のとき、\(\alpha \)を解として持つモニックな多項式を\(p(X)\)として、F係数の多項式の集合\(F[X] \)のイデアル
$$
J_{\alpha}=\{f(X) \in F[X] | f(\alpha)=0 \} = \bigl( p(X) \bigr)
$$
を考える。
イデアルは、ここでは詳しくは述べないが、\(p(X)\)の倍数全体の集合のことである。
この \(p(X)\) は \(\alpha\) を解に持つ多項式の中で、次数が最小のものとして取ることができる。
命題任意の多項式 \(f(X)\in F[X]\) について，
\[
f(\alpha)=0 \quad \Longleftrightarrow \quad p(X)\mid f(X)
\]
が成り立つ。
とくに、\(p(X)\)は\(F\)上、既約である。
証明
（\(\Rightarrow\)）
\(f(\alpha)=0\) と仮定する。
このとき，
\[
f(X)\in J_\alpha = (p(X))
\]
であるから，
ある \(q(X)\in F[X]\) が存在して
\[
f(X)=q(X)p(X)
\]
と書ける。
したがって，
\[
p(X)\mid f(X)
\]
が成り立つ。
（\(\Leftarrow\)）
\(p(X)\mid f(X)\) と仮定すると、ある \(q(X)\in F[X]\) が存在して
\[
f(X)=q(X)p(X)
\]
と書けるので、
\[
f(\alpha)=0
\]
が従う。
次に，\(p(X)\) が既約であることを示す。
\(p(X)\) が可約であると仮定し，
\[
p(X)=p_1(X)p_2(X)
\]
と分解できたとする。
ここで，
\(\deg p_1 \ge 1,\ \deg p_2 \ge 1\) とする。
両辺に \(\alpha\) を代入すると，
\[
0=p(\alpha)=p_1(\alpha)p_2(\alpha)
\]
となる。
体 \(E\) では零因子が存在しないため，
\[
p_1(\alpha)=0 \quad \text{または} \quad p_2(\alpha)=0
\]
が成り立つ。
仮に \(p_1(\alpha)=0\) とすると，
\[
p_1(X)\in J_\alpha
\]
である。
しかし，
\(\deg p_1 < \deg p\) であるから，
これは \(p(X)\) が
\(\alpha\) を解に持つ最小次数の多項式であることに矛盾する。
したがって，
\(p(X)\) は既約である。 ■
この \(p(X)\) は \(\alpha\) を解に持つ多項式の中で、
次数が最小の既約多項式であることがわかった。
この多項式 \(p(X)\) を、\(\alpha\) の
最小多項式という。
また、\(p(X)\) の次数を、\(\alpha\) の次数という。
単純拡大の様子
体 \(F\) と元 \(\theta\in E\) に対し，
\[
E=F(\theta)
\]
と書けるとき，
\(E\) を \(F\) の 単純拡大体 という。
体 \(F\) の中に \(\theta\) を添加し，
その四則演算で得られる数全体が \(F(\theta)\) である。
実は，
\(\theta\) が \(F\) 上代数的な元である場合，
体として生成することと，
環として生成することは一致する。
すなわち，
\[
F(\theta)=F[\theta]
\]
が成り立つ。
例
\[
\mathbb{Q}(\sqrt{2})
\]
を考える。
\(\sqrt{2}\) は \(\mathbb{Q}\) 上代数的であり，
\[
\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}
\]
と書けるため，
\(\mathbb{Q}[\sqrt{2}]\) はすでに体である。
したがって，
\[
\mathbb{Q}(\sqrt{2})=\mathbb{Q}[\sqrt{2}]
\]
が成り立つ。
定理（単純拡大の構造）\(\theta\) を \(F\) 上 \(n\) 次の代数的数とし、単純拡大\(E=F(\theta)\) とする。
このとき，
\[
E=F[\theta], \quad [E:F]=n
\]
が成り立つ。
また，
\[
\{1,\theta,\theta^2,\dots,\theta^{n-1}\}
\]
は \(E\) の \(F\)-基底である。
証明
\(\theta\) の \(F\) 上の最小多項式を
\[
p(X)=X^n+a_{n-1}X^{n-1}+\cdots+a_0\in F[X]
\]
とする。
このとき，
\[
J_\theta=\{f(X)\in F[X]\mid f(\theta)=0\}=(p(X))
\]
である。
\(p(X)\) は既約であり，
\(F[X]\) は単項イデアル整域であるから，
\((p(X))\) は極大イデアルである。
したがって，
\[
F[X]/(p(X))
\]
は体となる。（環の一般論より）
次に環準同型
\[
\varphi:F[X]\to F[\theta],\quad f(X)\mapsto f(\theta)
\]
を考える。
このとき，
\[
\ker\varphi=(p(X))
\]
であるから，準同型定理より
\[
F[X]/(p(X))\cong F[\theta]
\]
が成り立つ。
よって，\(F[\theta]\) も体であり，\(F(\theta)\)の最小性より
\[
F[\theta]=F(\theta)
\]
が従う。
任意の \(f(X)\in F[X]\) に対して，
多項式の除法より
\[
f(X)=q(X)p(X)+r(X),\quad \deg r\le n-1
\]
と書ける。
したがって，
\[
f(\theta)=r(\theta)
\]
であり，
\(F(\theta)\) の任意の元は
\[
a_0+a_1\theta+\cdots+a_{n-1}\theta^{n-1}
\quad (a_i\in F)
\]
と表される。
さらに，
\[
a_0+a_1\theta+\cdots+a_{n-1}\theta^{n-1}=0
\]
とすると，
次数 \(<n\) の多項式が \(\theta\) を零点に持つことになり，
最小多項式の定義に反する。
よって，
\[
\{1,\theta,\theta^2,\dots,\theta^{n-1}\}
\]
は一次独立であり，
\(F\)-基底である。
以上より，
\[
[E:F]=n
\]
が従う。■
例
\[
\mathbb{Q}(\sqrt{5})
\]
を考える。
\(\sqrt{5}\) の最小多項式は
\[
p(X)=X^2-5\in\mathbb{Q}[X]
\]
であり，
\[
[\mathbb{Q}(\sqrt{5}):\mathbb{Q}]=2
\]
である。
基底は
\[
\{1,\sqrt{5}\}
\]
であり，
\[
\mathbb{Q}(\sqrt{5})
=\{x+y\sqrt{5}\mid x,y\in\mathbb{Q}\}
\]
と表される。
分解体
方程式を解くとは、多項式 \(f(X)\) を完全に因数分解できる体を考えること。
すなわち，
\[
f(X)=a(X-\alpha_1)(X-\alpha_2)\cdots(X-\alpha_n)
\]
と表せるような数の世界（体）を考えたい。
このような体を
分解体
という。
分解体は、そもそも存在する？答えはYes。
それを保証するのが次の定理。
ある拡大体 \(E/F\) が存在して，\(f(X)\) は \(E[X]\) で\(n\)個の1次式に分解する。
証明
（方針）
商環により、根が存在するような体を作る。
そして、\(\deg f = n\) として，次数 \(n\) に関する帰納法で示す。
—
（i）\(n=1\) の場合
\[
f(X)=aX+b\quad (a\ne 0)
\]
と書ける。
このとき，
\[
X=-\frac{b}{a}\in F
\]
であるから，
\(f(X)\) はすでに \(F[X]\) において分解している。
—
（ii）\(n\ge 2\) の場合
\(f(X)\) が \(F[X]\) で既約であるとする。
このとき，
\(F[X]\) は単項イデアル整域であるから，
\((f(X))\) は極大イデアルであり，
\[
K:=F[X]/(f(X))
\]
は体となる。
商写像
\[
\varphi:F[X]\to K
\]
に対し，
\[
\xi:=\varphi(X)\in K
\]
とおく。
このとき，
\[
f(\xi)=\varphi(f(X))=0
\]
であるから，
\(\xi\) は \(f(X)\) の根である。
したがって，
\[
f(X)=(X-\xi)h(X)
\quad (h(X)\in K[X])
\]
と書ける。
ここで，
\[
\deg h = n-1
\]
である。
—
帰納法の仮定より，
\(h(X)\) はある拡大体 \(E/K\) において
一次因子に分解する。
このとき，
\(E/F\) も拡大体であり，
\[
f(X)=(X-\xi)(X-\alpha_2)\cdots(X-\alpha_n)
\quad (\alpha_i\in E)
\]
と完全に分解する。
—
以上より，任意の多項式 \(f(X)\in F[X]\) に対して，それが完全に分解する拡大体が存在する。■
まとめ
ここでは、ガロア理論の準備として、数の世界の拡大、つまり拡大体の性質についてまとめた。
この記事でわかったことをまとめると、
- 代数的元 \(\theta\) による体の拡大は単純拡大で表せる
- 代数的整数による\(F(\theta)\) は商環 \(F[X]/(p(X))\) と同型である
- 拡大次数は最小多項式の次数に一致する
- 多項式は必ず分解体をもつ
特に、多項式\(f(X) \in F[X] \)が体\(E\)で解けるとは、
\[
f(X)=(X-\alpha_1)(X-\alpha_2)\cdots(X-\alpha_n)
\quad (\alpha_i\in E)
\]
と因数分解できることであり、つまり、
\[
E=F(\alpha_1,\alpha_2,\cdots , \alpha_n)
\]
という数の世界を作れればよいが、このとき，\(\alpha_i\) は \(F\)の元の四則と冪 で作ればよい！！
==================================
にほんブログ村ランキングに参加しています.クリックで応援よろしくお願いします.
==================================