統計学で頻出の正規分布ですが,1変数はわかるのに多変数になると初見は面食らいます.
2変数の場合を例に上げながら多変量正規分布の数式の理解を目指したいと思います.
目次【本記事の内容】
多変量正規分布
まず,1変数の正規分布の定義式を眺めてみます.
この式を見れば,平均が\(\mu\)で,データのばらつき具合を表す分散が\(\sigma^2\)だと分かります.
指数関数\(exp\)の前に付いている係数\(\displaystyle \frac{1}{\sqrt{2\pi \sigma^2}}\)は全区間\(-\infty 〜 \infty\)で積分したときに全確率1となるようにつけたものです.この式を見ることで,データxの平均値やばらつき具合が分かり,xの分布が分かるという算段です.
ではこの式が多変数,n変数になった場合の式を見てみます.
まず,多変数の場合は,n個あるデータを1つの変数と見るため,データがn次元のベクトル表記になります.つまり,$$\vec{x}=\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n \\
\end{pmatrix}$$一つの要素\(x_i\)が確率変数\(X_i\)のデータを表します.
また,平均値\(\mu\)はn個のデータそれぞれに対して存在するため,こちらもn次元ベクトルです.
$$\vec{\mu}=\begin{pmatrix}
\mu_1 \\
\mu_2 \\
\vdots \\
\mu_n \\
\end{pmatrix}$$一つの要素\(\mu_i\)が確率変数\(X_i\)の平均を表します.
ここまでは,1変数の正規分布の値をベクトル表記にしただけです.
次に分散\(\sigma^2\)を考えます.
多変数の場合は,各データの分布だけでなく,データ間の相関も考慮する必要があります.下図の2変数の場合のように,\(x\)の増減と共に\(y\)がどのように増減するかの情報を入れることが1変数の場合との違いです.
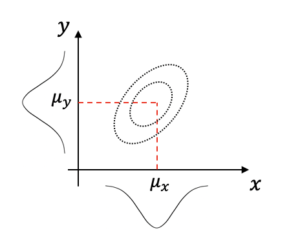
そのため,分散として,共分散を取り入れます.
次のような分散共分散行列\(\sum\)を定義します.
$$\sum =
\begin{pmatrix}
\sigma_1^2 & \sigma_{12} \cdots & \sigma_{1i} & \cdots & \sigma_{1n}\\
\sigma_{21} & \sigma_2^2 \cdots & \sigma_{2i} & \cdots & \sigma_{2n}\\
\vdots & \ddots & & & \vdots \\
\sigma_{i1} & & \sigma_{i}^2 & & \sigma_{in} \\
\vdots & & & \ddots & \vdots \\
\sigma_{n1} & \cdots & \sigma_{ni} & \cdots & \sigma_{n}^2
\end{pmatrix}
$$
見方としては,分散共分散行列の\((i,j)\)要素が確率変数\(X_i\)と\(X_j\)の共分散\(\sigma_{ij}\)です.
対角成分\((i,i)\)は確率変数\(X_i\)の分散\(\sigma_{i}^2\)です.
よって,1変数の指数部分\(\displaystyle -\frac{(x-\mu)^2}{2\sigma^2}\)に対して,\(\sigma^2\)を\(\sum\)に置き換えると,
\(|\vec{x}|^2={}^t\vec{x}・\vec{x}\)なので,
指数部分は,$$-\frac{1}{2}{}^t(\vec{x}-\vec{\mu}) {\sum}^{-1} (\vec{x}-\vec{\mu})$$とできます.
また係数部分は,\(\displaystyle \frac{1}{\sqrt{2\pi \sigma^2}}\)は\(2\pi\)部分をn個のデータ分でn乗して
\(\displaystyle \frac{1}{\sqrt{(2\pi)^n |\sum|}}\)
\(|\sum|\)は行列式です.
(係数はn重積分することで全確率が1となるようになっています.)
1変数の場合と同様に,式を見れば,平均がそれぞれ\(\mu_1,\mu_2, \cdots \)で,データのばらつき具合を表す分散と各データ間の共分散が分かります.
\(n=2\)における式展開
n=2の場合に,具体的に式を展開してみます.
確率変数を\(X,Y\)とします.
2変量正規分布を$$N_2 \left ( \begin{pmatrix}
\mu_x \\
\mu_y \\
\end{pmatrix} , \begin{pmatrix}
\sigma_{x}^2 & \sigma_{xy}\\
\sigma_{xy} & \sigma_{y}^2\\
\end{pmatrix} \right )=N_2 \left ( \begin{pmatrix}
\mu_x \\
\mu_y \\
\end{pmatrix} , \begin{pmatrix}
\sigma_{x}^2 & \rho\sigma_{x}\sigma_{y} \\
\rho\sigma_{x}\sigma_{y} & \sigma_{y}^2\\
\end{pmatrix} \right )$$
と書きます.ここで,\(\rho\)は\(X,Y\)の相関係数です.
この2変量正規分布を関数\(f\)で表すと,
平均\(\vec{\mu} = \begin{pmatrix}
\mu_x \\
\mu_y \\
\end{pmatrix}\)
分散共分散行列を\(\sum =
\begin{pmatrix}
\sigma_{x}^2 & \sigma_{xy}\\
\sigma_{xy} & \sigma_{y}^2\\
\end{pmatrix}=\begin{pmatrix}
\sigma_{x}^2 & \rho\sigma_{x}\sigma_{y} \\
\rho\sigma_{x}\sigma_{y} & \sigma_{y}^2\\
\end{pmatrix}\)
とおけば,$$f(\vec{x}) = \frac{1}{\sqrt{(2\pi)^2 |\sum|}}exp \left \{-\frac{1}{2}{}^t (\vec{x}-\vec{\mu}) {\sum}^{-1} (\vec{x}-\vec{\mu}) \right \}$$です.これより,\(X\)の分布は平均が\(\mu_x\),分散が\(\sigma_x^2\),\(Y\)の分布の平均が\(\mu_y\),分散が\(\sigma_y^2\),\(X,Y\)の共分散が\(\sigma_{xy}\),相関係数が\(\rho\)と読み取れます.
2変量正規分布を\(x,y\)の2変数の関数として具体的に書き表してみます.
\(|\sum| = \sigma_x^2\sigma_y^2-\rho^2\sigma_x^2 \sigma_y^2 = \sigma_x^2\sigma_y^2(1-\rho^2)\),
\(\sum^{-1} = \displaystyle \frac{1}{\sigma_x^2\sigma_y^2(1-\rho^2) }
\begin{pmatrix}
\sigma_{y}^2 & -\sigma_{xy}\\
-\sigma_{xy} & \sigma_{x}^2\\
\end{pmatrix} \).
\(∴ f(x,y)= \displaystyle \frac{1}{2\pi \sigma_x \sigma_y \sqrt{1-\rho^2}}\)
\(exp \left \{ \displaystyle -\frac{1}{2} (x-\mu_x,y-\mu_y) \displaystyle \frac{1}{\sigma_x^2\sigma_y^2(1-\rho^2)}
\begin{pmatrix}
\sigma_{y}^2 & -\sigma_{xy}\\
-\sigma_{xy} & \sigma_{x}^2\\
\end{pmatrix} \begin{pmatrix}
x-\mu_x \\
y-\mu_y \\
\end{pmatrix} \right \}\)
\(=\displaystyle \frac{1}{2\pi \sigma_x \sigma_y \sqrt{1-\rho^2}}\)
\(exp \left \{ \displaystyle -\frac{1}{2} \displaystyle \frac{1}{\sigma_x^2\sigma_y^2(1-\rho^2)}\{ \sigma_y^2(x-\mu_x)^2 – 2\sigma_{xy}(x-\mu_x)(y-\mu_y)+ \sigma_x^2(y-\mu_y)^2 \} \right \} \)
となります.
ここで,もし\(X,Y\)が無相関,つまり\(\rho = 0\)であれば,
\(f(x,y)=\displaystyle \frac{1}{2\pi\sigma_x \sigma_y} exp \left \{ \displaystyle -\frac{1}{2} \displaystyle \frac{1}{\sigma_x^2\sigma_y^2} \{ \sigma_y^2(x-\mu_x)^2+ \sigma_x^2(y-\mu_y)^2 \} \right \}\)
\(=\displaystyle \frac{1}{\sqrt{2\pi \sigma_x^2}\sqrt{2\pi \sigma_y^2}} exp \left \{ \displaystyle -\frac{(x-\mu_x)^2}{2\sigma_x^2}-\displaystyle \frac{(y-\mu_y)^2}{2\sigma_y^2} \right \}\)
\(=\displaystyle \frac{1}{\sqrt{2\pi \sigma_x^2}}exp \left \{-\displaystyle \frac{(x-\mu_x)^2}{2\sigma_x^2} \right \}・\frac{1}{\sqrt{2\pi \sigma_y^2}}exp \left \{-\frac{(y-\mu_y)^2}{2\sigma_y^2} \right \}\)
\(=f(x)・ f(y).\)
したがって,無相関(\(\rho=0\))であれば,2変数正規分布は独立で,\(X,Y\)それぞれの正規分布関数の積となります.
“独立”であれば”無相関”だが,一般に逆は成り立たちません.
しかし,多変量正規分布であれば,”独立”と”無相関”は同値です.
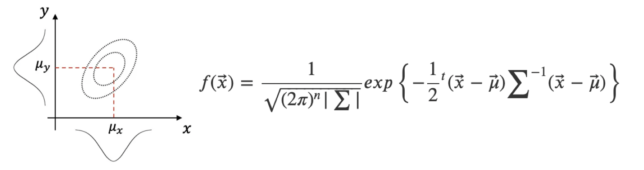
短大卒の僕に、こんな高度な数学を理解して他人に資料を説明させる世間は、どうなんでしょう?
でも、おかげさまでなんとなく流れは分かりました。
ありがとうございます
ノリオ様
コメントありがとうございます。
より分かりやすい記事を目指していきたいと思います。
今後もよろしくお願いいたします。