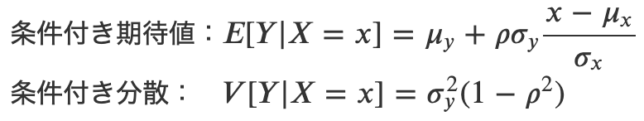2変量正規分布のXを固定したもとでの,条件付き確率分布および期待値と分散の公式を証明付きでまとめます.
統計検定準1級対策に.

２変量正規分布の条件付き期待値,分散の公式と覚え方

2変量正規分布\(f(x,y)\)の\(X=x\)の条件付き期待値と分散の公式です.

覚え方：
むやみに覚えても忘れてしまうので,意味づけをしながら覚えます.

条件付き期待値は,まずはYの期待値\(\mu_y\)があり,それにXの影響と相関の影響があると予測できます.Xの影響部分は,$$\displaystyle \frac{x-\mu_x}{\sigma_x}$$と標準化の形になっています.
相関の影響は,相関係数\(\rho\)とyの標準偏差\(\sigma_y\)が掛かると覚えましょう.

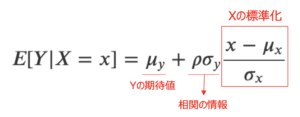
分散は,XとYの分散共分散行列\(\sum\)からXの分散情報を除いたものと覚えましょう.つまり,\(|\sum|=\begin{vmatrix}
\sigma_{x}^2 & \sigma_{xy}\\
\sigma_{xy} & \sigma_{y}^2\\
\end{vmatrix}
=\sigma_x^2\sigma_y^2(1-\rho^2)\)（ここで,\(\sigma_{xy}=\rho \sigma_x \sigma_y\)）
これを\(\sigma_x^2\)で割れば,$$V[Y|X=x]=\displaystyle \frac{|\sum|}{\sigma_x^2}=\sigma_y^2(1-\rho^2)$$と導くことができます.

証明①：条件付き確率分布を求める

公式の証明です.条件付き確率分布を求めます.

証明：
\(f(Y|X)=\displaystyle \frac{f(x,y)}{f(x)}=f(x,y)×\sqrt{2\pi}\sigma_x exp\left \{ \displaystyle \frac{(x-\mu_x)^2}{2\sigma_x^2}\right \}\)

ここで,2変量正規分布の確率密度関数\(f(x,y)\)は,
\(f(x,y)=\displaystyle \frac{1}{2\pi \sigma_x \sigma_y \sqrt{1-\rho^2}}\)
\(exp \left \{ \displaystyle -\frac{1}{2} \displaystyle \frac{1}{\sigma_x^2\sigma_y^2(1-\rho^2)}\{ \sigma_y^2(x-\mu_x)^2 – 2\sigma_{xy}(x-\mu_x)(y-\mu_y)+ \sigma_x^2(y-\mu_y)^2 \} \right \} \)
なので,（参照：多変量正規分布を理解する）代入すると,

\(f(Y|X=x)=\displaystyle \frac{\sqrt{2\pi}\sigma_x}{2\pi \sigma_x \sigma_y \sqrt{1-\rho^2}}\)
\(exp \left \{ \displaystyle -\frac{1}{2} \displaystyle \frac{1}{\sigma_x^2\sigma_y^2(1-\rho^2)}\{ \sigma_y^2(x-\mu_x)^2 – 2\sigma_{xy}(x-\mu_x)(y-\mu_y)+ \sigma_x^2(y-\mu_y)^2 \} \right \} \)
\(× exp\left \{ \displaystyle \frac{(x-\mu_x)^2}{2\sigma_x^2}\right \}\)
\(=\displaystyle \frac{1}{\sqrt{2\pi} \sigma_y \sqrt{1-\rho^2}} exp \left \{ \displaystyle -\frac{1}{2} ×A \right \} \)（指数関数の指数部分をまとめ一部をAとおきました.）

指数関数の中身のAを計算します.

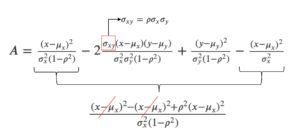
$$∴　f(Y|X=x)=\displaystyle \frac{1}{\sqrt{2\pi} \sigma_y \sqrt{1-\rho^2}} exp \left \{ \displaystyle -\frac{\{ y – (\mu_y +\frac{\rho \sigma_y}{\sigma_x}(x-\mu_x) \}^2}{2(1-\rho^2)\sigma_y^2} \right \}.$$

よって,公式を得ます.

■

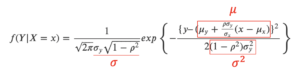
証明②：回帰分析による証明（期待値のみ）

\(x,y\)の単回帰分析を考えると,次のように単回帰直線が引ける.

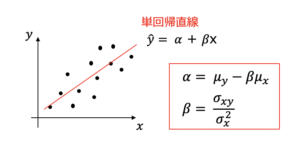
これを用いれば,
\(E[Y|X=x]=\alpha + \beta x\)
\(=(\mu_y-\beta \mu_x)+\beta x\)
\(=\mu_y-\displaystyle \frac{\sigma_{xy}}{\sigma_x^2} \mu_x+ \displaystyle \frac{\sigma_{xy}}{\sigma_x^2}x\)
\(=\mu_y-\displaystyle \frac{\rho \sigma_{x}\sigma_{y}}{\sigma_x^2} \mu_x+ \displaystyle \frac{\rho\sigma_{x}\sigma_{y}}{\sigma_x^2}x\)
\(=\mu_y+\rho \sigma_{y} \displaystyle \frac{x-\mu_x}{\sigma_x}\).

よって条件付き期待値を得る.

さいごに

条件付きの期待値や分散は統計検定準1級で実際に出題されています.
こういった基本公式は覚えておいて,試験では即座に使えるようにしておいた方がよいです.

もちろん,その背景にある導出を実際にやってみることや意味づけをして覚えることが重要です.

私も本で調べたりして自分で公式の導出を行い,府に落ちた上で公式として覚えました.

==================================

クリックで応援よろしくお願いします.

にほんブログ村