数列が収束する条件があると便利です.極限値は分からなくても,数列がCauchy(コーシー)列であれば,収束することが分かります.今後も使う非常に有用な定理です.今回はCauchy列が収束することを分かりやすく証明します.
なお,「東京大学出版 杉浦光夫著 解析入門1」を参考としております.
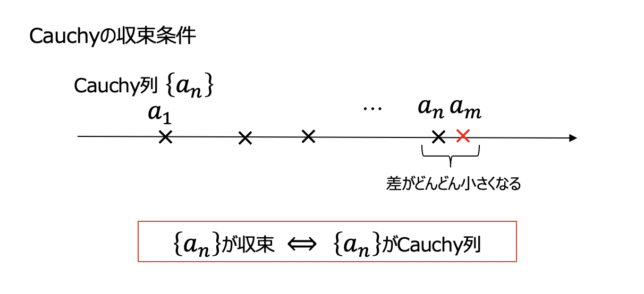
Cauchy(コーシー)列とは
つまりCauchy列とは,十分大きな項では,任意の項の差が十分小さくなるような数列のことです.
Cauchyの収束条件
この定理の素晴らしいところは,収束値が分からなくても,また複雑な数列でも,Cauchy列であることさえ示すことができれば,収束することの必要十分条件になることです.
Cauchy列の例
例:次の数列は収束するか?$$a_n = 1+\displaystyle \frac{1}{2^2}+\cdots +\displaystyle \frac{1}{n^2}$$
試行してみます.
\(a_1 = 1\)
\(a_2 = 1+\displaystyle \frac{1}{2^2}=1.25\)
\(a_3 = 1+\displaystyle \frac{1}{2^2}+\displaystyle \frac{1}{3^2}=1.361111111\cdots \)
\(a_5 = 1+\displaystyle \frac{1}{2^2}+ \cdots +\displaystyle \frac{1}{5^2}=1.4636111111\cdots \)
\(a_{10} = 1+\displaystyle \frac{1}{2^2}+ \cdots +\displaystyle \frac{1}{10^2}=1.54976773116654\cdots \)
\(a_{100} = 1+\displaystyle \frac{1}{2^2}+ \cdots +\displaystyle \frac{1}{100^2}=1.63498390018489\cdots \)
\(a_{1000} = 1+\displaystyle \frac{1}{2^2}+ \cdots +\displaystyle \frac{1}{1000^2}=1.64393456668156\cdots \)
この数列は収束するのかどうか,よく分かりません.
では,この数列がCauchy列であることを示します.
\(m \geq n\)として,
$$0\leq a_m-a_n = \displaystyle \frac{1}{(n+1)^2}+\displaystyle \frac{1}{(n+2)^2}+\cdots +\displaystyle \frac{1}{m^2}$$$$\leq \displaystyle \frac{1}{n(n+1)}+\displaystyle \frac{1}{(n+1)(n+2)}+\cdots +\displaystyle \frac{1}{(m-1)m}$$部分分数分解を行って,$$= \left ( \displaystyle \frac{1}{n} – \displaystyle \frac{1}{n+1} \right )+\left ( \displaystyle \frac{1}{n+1} – \displaystyle \frac{1}{n+2} \right ) \cdots +\left ( \displaystyle \frac{1}{m-1} – \displaystyle \frac{1}{m} \right )$$$$=\displaystyle \frac{1}{n}-\displaystyle \frac{1}{m}$$$$< \displaystyle \frac{1}{n}<\epsilon$$ (∵アルキメデスの原理より)
よって,この数列\(a_n\)はCauchy列であり,Cauchyの収束条件より収束することがわかった.
バーゼル問題
しかし,収束値については分かっていません.
この収束値を求める問題がかの有名な「バーゼル問題」と呼ばれ,苦心の末,1735年にレオンハルト・オイラーによって解かれました.
結果として,収束値は,$$1+\displaystyle \frac{1}{2^2}+\cdots +\displaystyle \frac{1}{n^2} \cdots = \displaystyle \frac{\pi^2}{6}$$です.
平方数の逆数の和を足していくと,円周率が出てくるとは驚きです.
ちなみに$$\displaystyle \frac{\pi^2}{6} = 1.644934066848226 \cdots$$で,先ほどの$$a_{1000} = 1+\displaystyle \frac{1}{2^2}+ \cdots +\displaystyle \frac{1}{1000^2}=1.64393456668156\cdots,$$$$a_{10000} = 1+\displaystyle \frac{1}{2^2}+ \cdots +\displaystyle \frac{1}{10000^2}=1.644834071848065\cdots,$$は確かに\(\displaystyle \frac{\pi^2}{6}\)に近付いています.
証明
では,Cauchyの収束条件を証明します.
十分条件(収束⇒Cauchy列)は容易に分かります.
必要条件(Cauchy列⇒収束)の証明は2ステップで行います.
①\(\{a_n\}\)が有界であること
②Cauchy列がある収束部分列の極限値に収束すること
これにはBolzano–Weierstrassの定理を使います.
証明:
十分条件(収束⇒Cauchy列):
数列\(\{a_n\}\)が収束しているので,収束値を\(\alpha\)として,$$\forall \displaystyle \frac{\epsilon}{2}>0,\exists N s.t. n \geq N \Rightarrow |a_n-\alpha|<\displaystyle \frac{\epsilon}{2}.$$∴$$m,n \geq N \Rightarrow |a_m-a_n|=|(a_m-\alpha)-(a_n-\alpha)|$$$$\leq |a_m-\alpha|+|a_n-\alpha|(∵三角不等式)$$$$<\displaystyle \frac{\epsilon}{2}+\displaystyle \frac{\epsilon}{2}=\epsilon.$$
必要条件(Cauchy列⇒収束):
①\(\{a_n\}\)が有界であること
\(\epsilon = 1\)として,$$\exists N s.t. m,n \geq N \Rightarrow |a_m-a_n|<1$$これより,\(m=n,n=N\)とすれば,\(|a_n-a_N|<1\)
$$∴ -1<a_n-a_N<1$$$$∴ a_N-1<a_n<a_N+1$$よって,\(M=\max \left \{|a_0|,|a_1|,|a_2|,\cdots,|a_N|,|a_N-1|,|a_N+1| \right \}\)とすれば,$$\forall n\in \mathbb{N},|a_n|\leq M$$$$∴ \{a_n\}:有界$$
②Cauchy列がある収束部分列の極限値に収束すること
①より\(\{a_n\}\)が有界なので,Bolzano–Weierstrassの定理から,\(\{a_n\}\)は収束する部分列\(\{a_{n(k)}\}\)をもつ.\(\displaystyle \lim_{k \to \infty}a_{n(k)}=\alpha\)とする.よって,$$\forall \displaystyle \frac{\epsilon}{2}>0,\exists k_0 s.t. k \geq k_0 \Rightarrow |a_{n(k)}-\alpha|<\displaystyle \frac{\epsilon}{2}.・・・(☆)$$
今,Cauchy列の条件より,$$\forall \displaystyle \frac{\epsilon}{2}>0,\exists N s.t. m,n \geq N \Rightarrow |a_m-a_n|<\displaystyle \frac{\epsilon}{2}.・・・(☆☆)$$
よって,\(m_0 = \max \{N,k_0 \}\)とすると,$$l\geq m_0 \Rightarrow |a_l-\alpha|=|(a_l-a_{n(l)})+(a_{n(l)}-\alpha )|$$
$$\leq |a_l-a_{n(l)}|+|a_{n(l)}-\alpha |(∵三角不等式)$$
$$<\displaystyle \frac{\epsilon}{2}+\displaystyle \frac{\epsilon}{2}=\epsilon.(∵(☆),(☆☆)より)$$
$$∴ \displaystyle \lim_{n \to \infty}a_n=\alpha.$$
■
ボルツァーノ・ワイエルシュトラスの定理の証明(解析学 第I章 実数と連続6)
まとめ(実数の連続性公理)
Dedekindの切断に関する実数の連続性公理から議論をスタートして,収束の定義によって今まで分かったことを次でまとめておきます.