微分積分は自然科学を語る上で無くてはならない宇宙の共通言語です.微分積分は高校数学で習いますが,実数や収束について厳密ではありません.本稿では,（自らの理解のために）実数の公理からはじめて,収束や微分・積分を定義し,項別微積分,広義積分等を厳密に理解することを目標とします.

なお,「東京大学出版　杉浦光夫著　解析入門１」を参考としております.

まず,世の中には自然数と四則演算があり,その過程で整数,分数（有理数）が認識された世界にいると考え,出発点とする.また,集合という概念と数の順序（不等号）は知っているとする.（どこまで厳密に定義するかを考えると,数学基礎論の話になりそうなので割愛もします。。。）

\(\sqrt2\)とは何か

いきなり抽象的な議論をすると難しいので,まずは身近な実数の例として\(\sqrt2\)を考えます.中学校で習う数ですが,分かっているようで実はよく分からない,\(\sqrt2\)は値にするとどのくらいなのか,どうやって計算するのか,存在性は保証されているのか,等という話をします.曖昧な理解になっているのは,無限（無限小）の話をちゃんと定義していないからです.微分積分は無限の話を扱うため,実数をきちんとした定義の上で理解する必要があります.

一辺が1の正方形の対角線の長さ\( x\)を考えると\(x\)はピタゴラスの定理より,
$$x^2 = 2 .$$この\( x\)を\(\sqrt2\)とする.つまり2乗して2になる数.では\(\sqrt2\)は,実際にはどのくらいの値なのか.だいたい,$$\sqrt2 = 1.4142\cdots $$くらいだとは分かるが,有理数では表せません（背理法で証明できる）.有理数が絶対だと思っていたピタゴラスはその有理数では表すことができない\(\sqrt2\)の存在を認めていませんでした（\(\sqrt2\)を発見した弟子を処刑したとか）.図形的には存在するのに,有理数では表せられない謎の数\(\sqrt2\).有理数を超えた新しい数として無理数という数が生まれました.

次の数列で\(\sqrt2\)の具体的な値に迫ってみます.$$a_{n+1} = \frac{1}{2}\displaystyle(a_n+\frac{2}{a_n}), a_1 =1$$数列\(a_n\)が収束することが前提ですが,仮に収束するとして\(n\)を十分大きくすると\(a_n\)と\(a_{n+1}\)はともに\(\alpha\)に収束するとする.すると$$\alpha = \frac{1}{2}(\alpha+\frac{2}{\alpha})$$よって,$$\alpha^2 = 2$$この数列は\(n\)をどんどん大きくすると\(\sqrt2\)になることが分かりました.具体的に書くと,$$1,1.5,1.41666\cdots,1.4142156\cdots,1.41421356\cdots$$これを永遠に続けると\(\sqrt2\)に近づきそうだが,そもそも近づいた先はどこにあるのだろうか.このように数列の近づいていく先を新たな数,無理数として考えられそうである.

次に数直線で\(\sqrt2\)の位置を考えてみます.\(\sqrt2\)は数直線上では,\(1.41\)と\(1.42\)の間にあることは分かります.それぞれ2乗すると\(1.9881\)と\(2.0164\)だから.

数直線上では何となく\(\sqrt2\)の位置は分かりますが,やはり曖昧な理解です.さて,ここでドイツの数学者Dedekind（デデキント：ゲッティンゲン大学）は数直線を\(\sqrt2\)の箇所で切断することを考えました.いきなり話が飛んだかもしれませんが,実数が連続的な数の並びなのであれば,切断した面で無理数が捉えられると考えられるわけです.

Dedekind切断と実数の連続性

Dedekind（デデキント）の切断は,数直線を切断した時に断面の数がどうなっているかで理解できます.

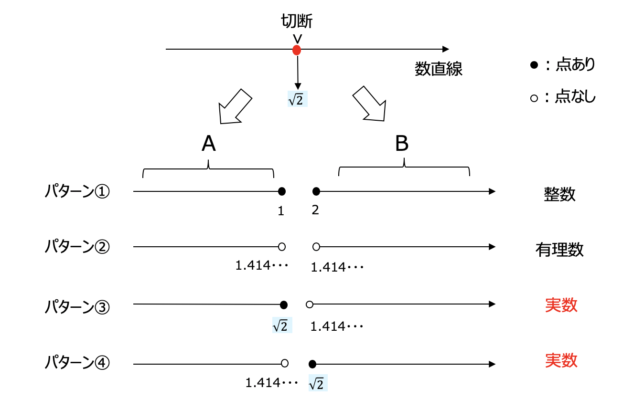
数直線を\(\sqrt2\)の点で２つの集合\(A,B\)に分けます（切断）.このとき,切断の断面が\(A\)側と\(B\)側にそれぞれできますが,次の４つのパターンが考えられます.

パターン①：
\(A\)側断面に点があり（\(A\)に最大元がある）,\(B\)側断面にも点があり（\(B\)に最小元がある）
→数を整数で考えるとこのようなことが起こります.
パターン②：
\(A\)側断面に点がなく（\(A\)に最大元がない）,\(B\)側断面にも点がない（\(B\)に最小元がない）
→数を有理数で考えるとこのようなことが起こります.
パターン③：
\(A\)側断面に点があり（\(A\)に最大元がある）,\(B\)側断面に点がない（\(B\)に最小元がない）
パターン④：
\(A\)側断面に点がない（\(A\)に最大元がない）,\(B\)側断面に点がある（\(B\)に最小元がある）
→このパターン③,④の場合は\(\sqrt2\)の存在を認めると起こります.

よって,Dedekindの切断を考えた場合,どこで切断してもパターン③か④しか起こり得ないような数が実数と言えそうです.

そこで,これを実数の公理「実数の連続性」とします.

では,Dedekindの切断と実数の連続性を数学的に（論理記号を使って）定義します.

これより,集合といえば,順序性を持った集合とします.

つまりDedekindの切断とは,集合\(K\) を部分集合\(A,B\)で順序を保った状態で漏れなくダブりなく分割することです.

つまり実数の連続性とは,集合\(K\) を切断<\(A,B\)>で分割したときに,どちらかの断面にだけ値がある状態ということで,これが有理数まででは表せない数字の存在を保証しています.
これはある意味,数を集合論的に捉えているということです.

最後に連続性の公理を上限という概念を用いてWeierstrassの流儀で言い換えたいと思います.
Weierstrass（ワイエルシュトラス）もドイツの数学者（ベルリン大学）で１９世紀に微分積分の厳密な基礎付けをされた方ですね.

Weierstrassの公理（実数の連続性の言い換え）

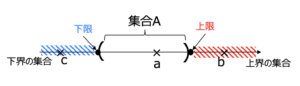
まず,上界（下界）と上限（下限）という概念を定義しておきます.

名前のとおり,その集合の全ての要素より大きい数が上界ということ.
（上界は\(A\)の元とは限らないし、上界は一般にたくさんある）

つまり,上限に対してちょっとでも数を引くと上界ではなくなるということ.

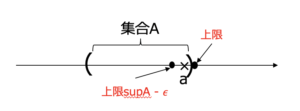
証明

\(\sup A\)は\(A\)の上界の中の最小元であるが,もし\(\sup A\)より小さい元である\(\sup A-\epsilon\)が上界となると\(\sup A\)の最小性に矛盾する.よって\(\sup A-\epsilon\)は\(A\)の上界ではないため,\(\forall a \in A , a \leq \sup A-\epsilon\)を否定して,命題を得る.

■

さて,準備が整ったため先ほどの連続性の公理を上限を用いて言い換える.

つまり,Weierstrassの公理とは上限が確かに存在するということを議論の出発点にするということ.

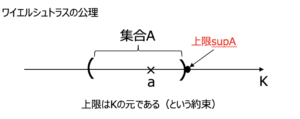
このWeierstrassの公理はDedekindによる連続性の公理の言い換えである.

証明

（\(\Rightarrow\))　集合\(K\)の部分集合\(A\)の上界の集合を\(B\)とする.\(C = B^C = K\setminus B \)とすると,<\(C, B\)>は\(K\)の切断である.Dedekindの公理より\(C\)の最大元または\(B\)の最小元がある.つまり\(A\)の上限が存在する.

（\(\Leftarrow\))　集合\(K\)の切断<\(A, B\)>を取ると,集合\(A\)は上界を持ち,Weierstrassの公理より上限\(s = \sup A\)が存在する.\(s \in A\)ならばDedekind切断のパターン③が成り立ち,\(s \notin A\)つまり\(s \in B\)ならばDedekind切断のパターン④が成り立つ.

■

以上より,実数の連続性は,Dedekindによる公理かWeierstrassによる公理どちらかで定義すればOKです.

数直線は繋がっているというイメージから定義を行いましたが,これを約束事として微分積分の演繹的で厳密な議論を行うことができるが数学の素晴らしさの一つだと思います.

==================================

クリックで応援よろしくお願いします.

にほんブログ村