大学で数学をやったことがある方であれば,ε-δ論法というものを聞いたことがあると思います.イプシロン-デルタ論法と読みます.これは何かというと,解析学で必要な“収束”という概念を扱うために必要な論法です.簡単にいうと,”どんどん近づく”と感覚を数学的に厳密に定義したものです.
今回はε-δ論法についてご説明します.
どんどん近づくということ
高校数学でも極限\(\lim\)というものを習いました.例えば,$$\lim_{x \to 0}2x = 0 $$これは,
\(x\)を\(0\)にどんどん近づけると,関数\(2x\)はどんどん\(0\)に近づく
ということを表しています.何当たり前のこと言ってんだこいつ,と思うかも知れませんが,私は高校生のときそう思っていました.これが何の役に立つのだろうと.実は大学に入って,より深い数学を学んだときに関数列の収束や微積分で当たり前のように出て来て,その論法の有り難みが分かるわけですが.
さて,先ほどの数式の意味は分かったと思います.では,関数\(2x\)が\(0\)に近づくとは,どのくらい近づいたら近いと判断できるのでしょうか.遠い,近いの定量的判断は？この辺りの疑問や感覚がはじめから備わっている方は,数学的センスがある方だと思います.
結論だけ述べると,
任意の数より差を小さくできるか
先ほどの定義を解説します.まずは$$|f(x)-b|<\epsilon$$に関してですが,εは今,任意と言っているので,例えば0.01とします.このとき,関数\(f(x)\)の値と\(b\)の距離である絶対値が0.01未満である,という意味です.
数と数の距離である差の絶対値が0.01未満ということは,その２つの数が近いと言えそうです.では,xがどうあればよいか.そこで,この与えられたεに対して,xとbの距離（差の絶対値）をどのくらいにすればよいかが\(|x-a|<\delta\)です.
つまり,与えられたεという近さの指標に対して,xとaの距離がδ未満であれば満足するということです.
ε-δ論法は後出しジャンケン
では,定義に従って\(\displaystyle \lim_{x \to 0}2x = 0\)を考えます.例えば,2xと0の距離εを0.01未満にしたいと思います.そうすれば0に近づいたと言えそうです.つまり,$$|2x-0|=2|x|<0.01$$これを満足するには,$$|x-0|=|x|<0.005$$となればよいことが分かります.よって,δとして0.005と取ればよいです.いや0.01では近いとは言えない,0.00001未満にならないと,となればδを0.000005とすればよいわけです.つまり近さの指標εは人それぞれですが,誰かが提示した小さな値εに対して,後から満足するようなδを提示すればよいわけなので,ε-δ論法は後出しジャンケンと一緒です.
実際には,誰かが距離をε未満にしろと言えば,δとして,$$\delta = \frac{\epsilon}{2},|x-0|<\delta$$とすれば,$$|2x-0|=2|x| < 2\frac{\epsilon}{2} = \epsilon$$とできて,$$\displaystyle \lim_{x \to 0}2x = 0$$は正しいということが分かりました.
数列の極限
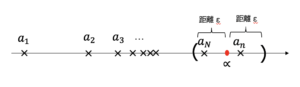
これは数列の極限でも同じです.数列\(a_n\)が値\(\alpha\)に近づく,つまり\(\displaystyle \lim_{n \to \infty} a_n = \alpha\)であるとは, 任意の正の実数\(\epsilon\)に対して,ある自然数\(N\)が存在し,\(n \geq N\)のとき,\(|a_n-\alpha|<\epsilon\)となる.
つまり,先ほどのδの代わりに数列をN番目より大きなものにすると近さの指標εを満足するということです.これはε-N論法といいます.
論理記号
任意の〜は\(\forall\)で表し,ある・存在するは\(\exists\),このときはs.t.(such that)という記号を使った方が文章も完結になり美しいです.
ε-δ論法を理解するには
こういった論法は慣れないと最初はよく分かりません.自分で図を書いて理解する,極限の証明問題（はさみうちの原理等）を手を動かして理解していくことで少しずつ腑に落ちていきます.私はそうやって徐々に慣らしていきました.今ではむしろ論理記号でε-δ論法が書かれていた方が安心します.
高校数学の極限においてもε-δ論法やε-N論法を出しても良いと個人的には思っております.論理記号の練習になりますし,教科書は結構あやふやな定義しか書いておらず,センスのある学生は逆に混乱してしまうのではないですかね.
==================================
にほんブログ村ランキングに参加しています.クリックで応援よろしくお願いします.
==================================