統計学では様々な確率分布を考える際に,母集団のパラメーターを推定する必要があります.そのときの良い推定とは何でしょうか？
基準となる一致性,不偏性について紹介します.

母集団のパラメーターとは？

例えば,調べたいデータの分布が正規分布に従っていると仮定します.

このとき,正規分布の形を決めるには,母集団の平均\(\mu\)と分散\(\sigma^2\)を知る必要があります.このときの平均や分散を母集団のパラメーター（または母数）といいます.

ポアソン分布の場合は,平均が分布を決めるパラメーターとなります.

しかし,母集団の全てを知ることは現実的に不可能なので,サンプルを抽出します.そのサンプルから母集団のパラメーターを推定することになります.

例えば,「サンプルたちの平均をとると,だいたい母集団の真の平均に近いのでは？」などと推定するわけです.

とは言っても,どういう推定が本当に良い推定値と言えるのでしょうか.

その推定値が良いのか悪いのか,科学的な指標が欲しいのです.

何をもって良い推定とするか？一致性と不偏性

まず取得するサンプルの数を増やせば増やすほど,真のパラメーターに近づいていく推定値は良いと言えそうです.

例えば,サイコロで1の目が出る確率を出そうとした場合,サイコロを何回か振って,1の目が出た平均をとります.

これは大数の法則より,サンプルの数を増やせば\(\displaystyle \frac{1}{6}\)に近き,真の値にも近づきます.
つまり目の平均は,サンプルの数を増やせば増やすほど真のパラメーターに近づく良い推定値となります.

このような推定値の条件を一致性といいます.

数式で定義すると,真のパラメーター\(\theta\)に対し,サンプル数\(n\)から計算される推定値\(\hat{\theta}_n\)が一致性推定量とは,$$P(|\hat{\theta}_n – \theta|<\epsilon) \to 1(n \to \infty)$$

この式で計算するような問題は,統計検定準1級までには出てこないと思われますが,サンプル数を増やすと,真の値に収束するということを覚えておけば良いでしょう.

次に考えられることとして,不偏性があります.

サンプルから計算した推定値はランダムにとったサンプルのため確率的な値となりますが,ある程度,真の値近くに分布した確率値であれば,推定値として良いと言えそうです.

つまり,サンプルによって計算された推定値は真の値近くである確率が高く,期待値としては真の値になることが求められます.

このような推定値の条件を不偏性といいいます.

数式で定義すると,真のパラメーター\(\theta\)に対し,サンプルから計算される推定値\(\hat{\theta}\)が不偏推定量とは,$$期待値E[\hat{\theta}]=\theta$$

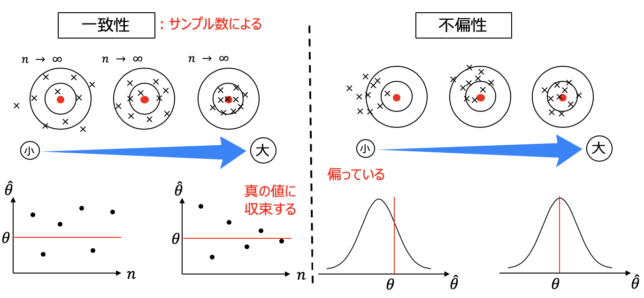
・一致性はサンプルの数を増やすと真のパラメーターに収束する,
・不偏性は期待値が真のパラメーターになる

ということで下の図と共に覚えておきましょう.

一致性,不偏性の例

最後に,一致推定量と不偏推定量の例です.

一致推定量：

標本平均\(\bar{X}=\displaystyle \frac{1}{n} \displaystyle \sum_{i=1}^{n}X_i\)は平均\(\mu\)の一致推定量.
標本分散\(\displaystyle \frac{1}{n} \displaystyle \sum_{i=1}^{n}(X_i-\bar{X})^2\)は分散\(\sigma^2\)の一致推定量.
不偏分散\(\displaystyle \frac{1}{n-1} \displaystyle \sum_{i=1}^{n}(X_i-\bar{X})^2\)は分散\(\sigma^2\)の一致推定量.

不偏推定量：
標本平均\(\bar{X}=\displaystyle \frac{1}{n} \displaystyle \sum_{i=1}^{n}X_i\)は平均\(\mu\)の不偏推定量.
不偏分散\(\displaystyle \frac{1}{n-1} \displaystyle \sum_{i=1}^{n}(X_i-\bar{X})^2\)は分散\(\sigma^2\)の不偏推定量.

標本分散は分散の不偏推定量にはならず,不偏分散が分散の不偏推定量になります.以下で証明しています.

サンプル平均の期待値,分散,不偏推定量まとめ（統計検定準1級対策2）

さらに,サンプル平均$$\bar{X}=\displaystyle \frac{1}{n} \displaystyle \sum_{i=1}^{n}X_i$$は不偏な推定量の中でも分散が最小となる最良線形不偏推定量（BLUE）です.

==================================

クリックで応援よろしくお願いします.

にほんブログ村