前回,有理数では説明のできないルートなどを説明しようと実数の連続性公理を約束毎と決めました.今回は実数の定義を行い,\(\sqrt 2\)が存在することを保証します.つまり,四則演算や実数の連続性公理さえ認めてれば,矛盾なく解析学の体系を説明できるということです.

なお,「東京大学出版　杉浦光夫著　解析入門１」を参考としております.

実数\(\mathbb{R}\)の定義

実数というのは高校では有理数以外の無理数（ルート）,超越数（円周率\(\pi\)）まで含めた数と教わりました.私もこれに特に疑問を持つことなく過ごしていました.大学以降,厳密な微分積分を行うために,実数をきちんと定義する必要があると分かりました.実数の定義とは四則演算と計算に関するちょっとしたルールに加え,前回まとめた実数の連続性公理を含めます.

この(1)〜(8)までは今までやっていた四則演算とか０とか負の数,不等号のことを言っているだけです.(7)の逆元とは、掛けて1になる数のことです.

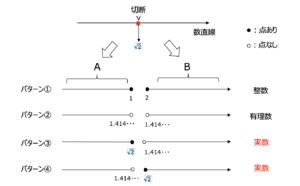
(8)までは有理数までの話.ところがこれでは\(\sqrt2\)がうまく説明できないので、(9)の実数の連続性公理を実数の定義とします。実数の連続性公理は,数直線というものが切れ目なく繋がっているのであれば,どこかで切断すると一片の切断面にある点があり,もう片方の切断面はある点に近づくけどその点ではない状態のこと.もし両断面に点が現れるのは,その両断面の点の間の点で切断されてしまっているから連続じゃない.またもし,両断面とも定まった点が無いのは,収束点が無いと言えます.

実数の定義から導けること（マイナス×マイナス＝プラスなど）

さて、この定義だけで次を証明したいと思います.

どれも当たり前に使っているようなきがしますが,これも先の実数の定義から全て導けてしまいます.④や⑥は何でマイナスにマイナスかけるとプラスになるんだという話ですね.ではやってみます.

① 和に関して\(-a\)の逆元が存在するため定義より\((-a) + {-(-a)} = 0\). 両辺に\(a\)を加えると,\(-(-a) = a \).
② \(0・a = (0+0)・a\)(∵ 零元の定義(２)より)\(=0・a+0・a=0\).(∵ 分配法則より).
③ \((-1)・a + a = \{(-1)+1\}・a = 0・a = 0\). ∴\((-1)・a = -a\).
④ \((-1)・(-1) = -(-1)\)(∵ ③より)\( = 1\)(∵ ①より)
⑤ \(a・(-b) + ab = a(-b + b) = a・0 \).　∴\(a・(-b) = -(ab) = (-a)・b\).
⑥ \((-a)・(-b) = -(a・(-b)=-(-(ab)) = ab\).
⑦ もし\(b \neq 0\)とすると,逆元\(b^{-1}\)が存在して,\(a = a・1 = ab・b^{-1} = 0・b^{-1} = 0\).
⑧ \((-a)・{-(a^{-1})} = -(-(a・a^{-1}) = a・a^{-1} = 1\).　∴ \(-a\)の逆元は\(a^{-1}\)の負の数.

■

当たり前のことを約束毎に従って式変形しただけですが,大事なことは数学は公理,定義と演繹的議論の繰り返しで成り立っているとうことです.

では,\(\sqrt2\)が実数の中に存在することを次で保証します.

平方根の存在保証

証明

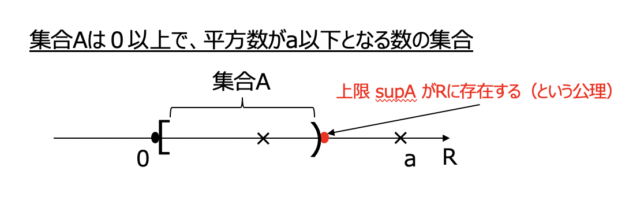
$$A = \{x \in \mathbb{R} | x \geq 0, x^2 \leq a \}$$とおく.\(A\)には\(0\)が属するため空集合ではない.\(A\)は上に有界な集合である.なぜなら,\(a > 1\)ならば\(a\)が\(A\)の上界になるし,\(a \leq 1\)ならば,\(1\)が\(A\)の上界になる.(∵ \(\forall x \in A , x^2 \leq a \leq 1 = 1^2\)となり, \( x \leq 1\)だから.)

ここで,Weierstrassの連続性公理を使います.

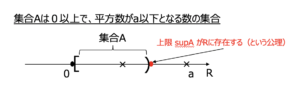
公理より,上に有界な集合\(A\)には上限\(\sup A \in \mathbb{R} \)があり,それを\(b\)とすると,
$$b^2 = a .$$
実際,\(b^2 < a\)とすると,次のような矛盾が出る.\(\epsilon = \min \left \{b,\displaystyle \frac{a-b^2}{3b}\right \}\)とおく.\(\epsilon > 0\)である.よって,\(b\)と\(b+\epsilon\)の大小を評価すると,
$$b^2 < (b+\epsilon)^2$$ $$ = b^2 + 2b\epsilon + \epsilon^2 \leq b^2 + 2b\epsilon + b\epsilon$$ $$ = b^2 + 3b\epsilon \leq b^2 + 3b\cdot \displaystyle \frac{a-b^2}{3b} = a.$$ よって,\(b+\epsilon \in A\)となるが,これは\(b\)が\(A\)の上限であることと矛盾する.同様に,\(b^2 > a\)と仮定すると,\(\epsilon = \min \left \{b,\displaystyle \frac{b^2-a}{3b}\right \}\)とおく.
$$b^2 > (b-\epsilon)^2$$ $$ = b^2 – 2b\epsilon + \epsilon^2 \geq b^2 – 2b\epsilon \geq b^2 – 3b\epsilon$$ $$ = b^2 – 3b\epsilon \geq b^2 – 3b\cdot \displaystyle \frac{b^2-a}{3b} = a.$$
一方,\(b-\epsilon\)は既に\(A\)の上界ではなくなっているので,\(\exists x \in A , b-\epsilon < x\)となり,\((b-\epsilon)^2 < x^2 \leq a\).これも上の不等式と矛盾.以上より,\(b^2=a\)となる.

■

これで,実数の連続性公理から初めてやっと平方根の存在を言うことができました.ただし,具体的な値の求め方はまた別の話です.数学ではこういう定理がよくあります.

==================================

クリックで応援よろしくお願いします.

にほんブログ村