循環小数とは小数点以下のある位から同じ数字の列が無限に繰り返される小数です.

例えば \(0.333\cdots\) や \(6.123123123\cdots\)です.

繰り返す数字の初めと終わりの上に「・」を付けて循環することを表します.

$$0.\dot{3}  = 0.333\cdots$$

\[ 6.\dot{1}2\dot{3}  = 6.123123123\cdots\]

循環小数を分数で表す方法, つまり割り算で循環小数を作る方法を紹介します.

循環小数を分数で表す

循環小数の部分をうまく消すことがポイントです.

解

(1)　\(x = 0.\dot{3}\)として, 両辺を１０倍すると \(10x = 3.\dot{3}\)

$$x = 0.333 \cdots　・・・　①$$

$$10x = 3.333 \cdots　・・・　②$$

②-①より, \(9x = 3 \)（循環小数部分がうまく消えている）
よって,
$$x = \frac{3}{9} = \frac{1}{3} $$

このように、10倍して小数点をスライドさせ,元の数を引くと循環小数部分が消え, あとは一次方程式を解くだけとなります.

(2)は何倍すればよいでしょうか.
\(x = 6.\dot{1}2\dot{3} \)として, 両辺を1000倍すると \(1000x = 6123.\dot{1}2\dot{3}\)

$$x = 6.123123123 \cdots　・・・　①$$

$$1000x = 6123.123123 \cdots　・・・　②$$

②-①より, \(999x = 6117 \)（6123から6を引くのを忘れないように）
よって,
$$x = \frac{6117}{999} = \frac{2039}{333} $$

■

検算として,試しに\(\frac{2039}{333}\)を計算してみると,

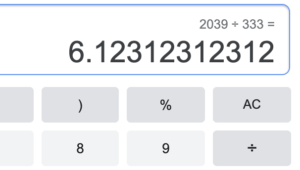
正しく得られました.このように循環小数は分数で表すことができます.パッと見ではどういう割り算で循環する小数が得られるかわかりませんが,アルゴリズム的に分数が得られるのは面白いと思います.
では,循環小数かどうか分からなくても,無限に続くような小数を分数で表すことはできるでしょうか.

発展〜有理数と無理数〜

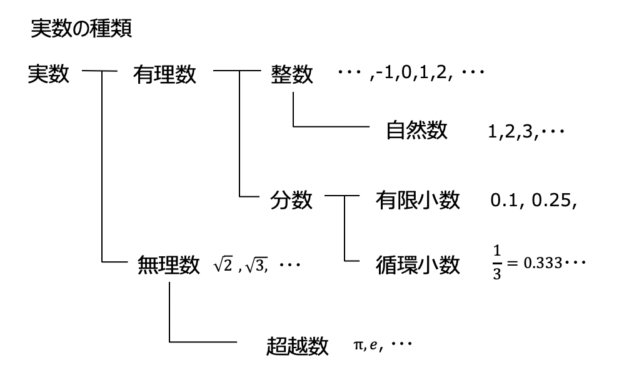
数（実数）というのは次のように分けることができます.

有理数（自然数,整数,有限小数,循環小数）は全て分数で表すことができます.無理数（ルートや円周率）は分数で表すことができません.

実数を捉えるには連続性という考えを理解する必要があります.連続性とは,切れ目なく繋がっていることをいい, 高校までは数直線として教わります.数直線はどこをとってもみっちりと数があります.\(0.00 \cdots 1 \)という有理数だけでも数直線を表していそうですが,全然穴だらけです.

18世紀ニュートンとライプニッツによって始まった微積分学は無限小を捉えるものですが,厳密な証明の為には実数の本質「連続性」を調べる必要がありました.その上に厳密な解析学ができています.そのおかげで今の数学および世の中の技術が成り立っていると思うと感慨深いものがあります.

循環小数を等比無限級数で理解する

循環小数は高校数学で習う無限等比級数で理解できます.

1.の\(6.\dot{1}2\dot{3} \)を足し算に分解してみると
$$6.123123 \cdots = 6 + 0.123 + 0.000123 + 0.000000123 \cdots$$
$$= 6 + 0.123 + 0.123 \times \frac{1}{10^3} + 0.123 \times \frac{1}{10^6} + \cdots$$
$$= 6 + \sum_{n=1}^{\infty} 0.123・(10^{-3})^{n-1}$$
これは初項0.123, 公比\(10^{-3}\)の無限等比級数で,公比が１より小さいので収束して
$$= 6 + \frac{0.123}{1-10^{-3}}$$
$$= 6 + \frac{123}{999}$$.

つまり,次がいえる.

==================================

クリックで応援よろしくお願いします.

にほんブログ村