我々は今,実数の連続性を公理とし,数列の極限について定義,様々な極限操作を論理的に厳密に扱えるようになりました.
そして,数列の収束を判定するCauchyの収束判定条件を証明しました.
実は,アルキメデスの原理を加えれば,これははじめに仮定した「実数の連続性公理」と同値なのです.
今回はこれを証明します.
なお,「東京大学出版 杉浦光夫著 解析入門１」を参考としております.
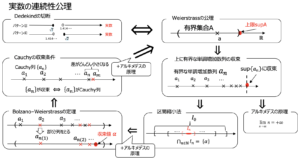
実数の連続性公理
まず,我々が解析学の議論の出発点とした「実数の連続性公理」をおさらいします.
二つの同値な公理を採用しました.
Dedekind切断による実数の定義とWeierstrass流の有界集合には上限が実数内に存在するというものでした.
ここではWeierstrassの連続性公理を使います.
このWeierstrassの公理はDedekindによる連続性の公理と同値です.
議論の出発点〜実数の連続性とは？〜（解析学 第I章 実数と連続１）
Cauchyの収束条件から連続性公理を導く
Cauchy列についておさらいします.
アルキメデスの原理は\(\displaystyle \lim_{n \to \infty}\displaystyle \frac{1}{n}=0\)を保証しています.
有界な単調増加数列の収束先は？アルキメデスの原理の証明（解析学 第I章 実数と連続4）
これらの定理は,実数の連続性公理から導かれる結果です.
逆に,「Cauchyの収束条件」と「アルキメデスの原理」から,「Weierstrassの公理」を導きます.
\(\Longrightarrow\) 「Weierstrassの公理」が成り立つ.
証明：
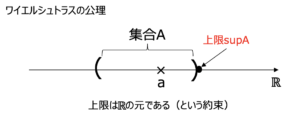
\(A\subset \mathbb{R}\)を空でない有界な集合とする.
\(A\)の上限\(\sup{A}\)が存在することを示す.
\(A\)の上界の集合を\(B\)とし,\(C=B^c=\mathbb{R}＼B\)とする.\(A\)は上に有界なので,\(B\neq \emptyset\)である.\(C\)は\(A\)の上界ではない実数の集合である.
任意の\(b \in B,c \in C\)に対して,\(\exists a \in A s.t. c<a\leq b.\)
これは,\(A\)に最大限があった場合,その最大限は\(B\)の元になるから成り立つ.
今,\(b_0 \in B,c_0 \in C\)を１つずつとり,以下のように帰納的に数列\(\{ b_n \},\{ c_n \}\)をつくる.
$$d_n = \displaystyle \frac{b_n+c_n}{2}$$とし,\(d_n \in B\)ならば,$$b_{n+1}=d_n,c_{n+1}=c_n$$\(d_n \in C\)ならば,$$b_{n+1}=b_n,c_{n+1}=d_n$$このとき,\(c_n\leq d_n \leq b_n\)なので,\(\{b_n\}\)は単調減少数列,\(\{c_n\}\)は単調増加数列となる.
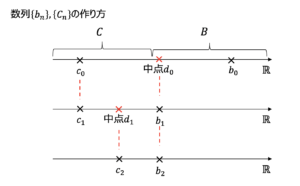
実は,数列\(\{ b_n \},\{ c_n \}\)はCauchy列である.
（∵）
自然数\(n\)より大きい\(p,q\)番目の項に対して,$$|b_p-b_q|\leq b_n-c_n\leq \displaystyle \frac{b_0-c_0}{2^n}\longrightarrow 0 (n \to \infty)・・・（☆）$$最後の収束はアルキメデスの原理より成り立つ.同様に,$$|c_p-c_q|\leq b_n-c_n\leq \displaystyle \frac{b_0-c_0}{2^n}\longrightarrow 0 (n \to \infty)$$であるので,数列\(\{ b_n \},\{ c_n \}\)はCauchy列である.
さて,Cauchy列は収束するので,$$\displaystyle \lim_{n \to \infty}b_n=b,\displaystyle \lim_{n \to \infty}c_n=c$$である.(\(b,c\)は適当な実数.)
ここで,上記の（☆）より,$$\displaystyle \lim_{n \to \infty}(b_n-c_n)=\displaystyle \lim_{n \to \infty}b_n-\displaystyle \lim_{n \to \infty}c_n=0$$$$∴ b=c.$$
実は,\(\sup{A}=b\)である.
(∵)
上限であることを示すには,\(b\)より小さい元が\(A\)の元になること,つまり,\(\forall x<b,\exists a \in A s.t. x<a\)を示せばよい.
\(\forall a \in A\)に対して,\(a\leq b_n\)より,\(a\leq b\)となり,\(b\)は\(A\)の上界である.
\(b\)より小さい任意の元\(x\)に対して,$$\lim_{n \to \infty}c_n=c=b\)より\(n\)を十分大きくすれば,\(x<c_n\)となる.
\(c_n\)は\(C\)の元で,\(A\)の上界ではないので,\(\exists a \in A s,t. c_n<a\)とできる.
したがって,$$x<c_n<a\leq b.$$
これより,\(\forall x<b\)に対しては,\(A\)の上界ではなくなってしまうことが分かり,\(\sup{A}=b\)であることが示せた.
これはWeierstrassの実数の連続性公理のことである.
■
まとめ（実数の連続性公理）
Dedekindの切断に関する実数の連続性公理から議論をスタートして,収束の定義によって今まで分かったことを次でまとめておきます.
==================================
にほんブログ村ランキングに参加しています.クリックで応援よろしくお願いします.
==================================