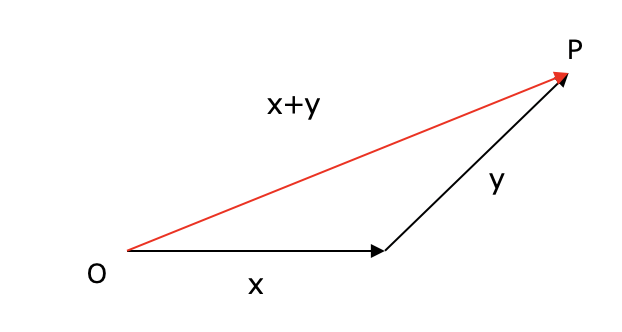
不等式の問題でよく出る「三角不等式」というものがあります.角を曲がるのではなくて最短距離を斜めに横断した方が断然早いという一見当たり前なものですが,様々なバリエーションがあり,奥が深いです.また数列の極限の評価等によく使われます.様々なバリーションはたまに忘れてしまうので,まとめておきます.

三角不等式

三角不等式の覚え方

まず,基本となる下記の不等式を覚えます.そしてこれは直感的に当たり前です.

これは,ある地点まで行くのに,最短距離をまっすぐ行くより,角を曲がる方が余計かかると言っています.

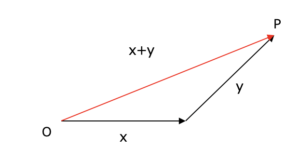
左の図のように地点Oから地点Pまで行くのに,ベクトルx進んで,ベクトルy進むより,赤線のようにまっすぐベクトルx+yという道を通った方が距離が短い.

次にこれから,以下を導きます.公式の丸暗記というより最小限の公式から都度導いた方が間違えも少なく,また応用も効いてよいです.私は高校生のとき,公式は基本的な物だけ覚えて,あとはほとんど試験中に作っていました.

証明：
三角不等式①より,\(|(x+y)-y| \leq |x+y|+|-y| = |x+y|+|y|\).左辺は\(|x|\)のことなので,\(|x| \leq |x+y|+|y|\).移項することによって,$$|x|-|y| \leq |x+y|$$

■

これも,図形的に考えて見ると,ベクトルx進んで,ベクトルy戻るので,総移動距離x-yとしては出発点Oとあまり変わらないと言えそうです.

以上より,(1)の不等式$$(1)　|x|-|y| \leq |x+y| \leq |x|+|y|$$がいえました.あとは,真ん中の絶対値の中身の符号をマイナスに変えたものも成り立つと覚えます.$$(2)　|x|-|y| \leq |x-y| \leq |x|+|y|$$

これも基本の三角不等式①から導けるようにします.

証明：
三角不等式①に対して,$$x+y=z$$とすると,$$x=z-y$$①に代入すると,$$|z| \leq |z-y| + |y|$$$$∴　|z|-|y| \leq |z-y|$$また,$$|z-y|=|z+(-y)| \leq |z|+|-y| = |z|+|y|$$以上より,\(z\)を\(x\)と書けば$$|x|-|y| \leq |x-y| \leq |x|+|y|$$

基本の三角不等式の証明

最後に基本となった三角不等式①を3パターンで証明します.

証明１：絶対値の定義から
絶対値の定義は$$|x|=\max \{x,-x\}$$です.符号が負であれば符号をとるものです.よって,$$-|x| \leq x \leq |x|, -|y| \leq y \leq |y|$$両辺足すと,$$-(|x|+|y|) \leq x+y \leq |x|+|y|$$これにマイナスを掛けると次も言える.$$-(x+y) \leq |x|+|y|$$以上より,$$|x+y| = \max \{x+y, -(x+y)\} \leq |x|+|y|$$

■

証明２：代数的に計算
$$（右辺）^2 – (左辺)^2 = (|x|+|y|)^2 – (|x+y|)^2$$$$=|x|^2+2|x||y|+|y|^2-(x+y)^2$$$$=x^2+2|x||y|+y^2-x^2-2xy-y^2$$$$=2(|xy|-xy) \geq 0$$ここで,\(|x|+|y| \geq 0, |x+y|\geq 0\)より,$$|x|+|y| \geq |x+y|$$
等号成立条件は,\(|xy|=xy\)なので,\(xy \geq 0\)

■

証明３：ベクトルとして
\(x,y\)をベクトル\(\vec{x},\vec{y}\)として示す.
$$（右辺）^2 – (左辺)^2 = (|\vec{x}|+|\vec{y}|)^2 – (|\vec{x}+\vec{y}|)^2$$$$=|\vec{x}|^2+2|\vec{x}||\vec{y}|+|\vec{y}|^2-|\vec{x}|^2-2\vec{x}・\vec{y}-|\vec{y}|^2$$$$=2(|\vec{x}||\vec{y}|-\vec{x}・\vec{y})$$

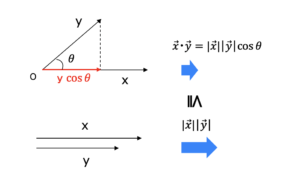
ここで最後の式は,コーシー・シュワルツの不等式より\(\geq 0\)が言える.コーシー・シュワルツの不等式はベクトルの内積に関する不等式です.内積を物理の力と考えれば,２つのベクトル\(\vec{x},\vec{y}\)で物を引っ張る力は,その２つのベクトルが同じ方向を向いている方が大きくなると言っています.

■

まとめ

三角不等式の様々なバリエーションは不等式の評価でよく出てきます.基本となる三角不等式から即座に導けるようにしておきたいところです.特に解析学では,収束値を求める際に,ε-δ論法でよく現れます.

例えば,下記記事の数列の極限に関する命題の証明で使っています.

数列が収束するとは？数列の収束の計算方法について解説（解析学 第I章 実数と連続３）

==================================

クリックで応援よろしくお願いします.

にほんブログ村