有界な数列は常に収束する部分列を持つこと保証する「ボルツァーノ・ワイエルシュトラスの定理」を分かりやすく証明します.
n次元に一般化した際に有界閉集合の本質に繋がる重要な定理です.
なお,「東京大学出版 杉浦光夫著 解析入門1」を参考としております.
ボルツァーノ・ワイエルシュトラスの定理
定理(ボルツァーノ・ワイエルシュトラスの定理)
有界な実数列\(\{a_n\}\)は常に収束する部分列をもつ.
部分列とは,数列の項を部分的に無限個取って作った数列です.ただし,項の順番は変えません.
数列\(\{a_n\}_{n \in \mathbb{N}}\)に対して,部分列の\(k\)項目に,ある自然数\(n(k)\)を対応させて,部分列を$$\left \{a_{n(k)}\right \}_{k \in \mathbb{N}}$$で表します.
ボルツァーノ・ワイエルシュトラスの定理のイメージです.
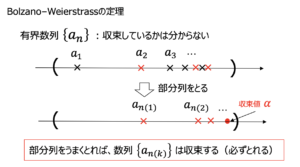
収束する部分列の例
(1)元の数列\(\{a_n\}\)が収束するのであれば,任意の部分列\(\left \{a_{n(k)}\right \}\)もその値に収束します.
(∵)\(\displaystyle \lim_{n \to \infty}a_n = \alpha\)とすると,\(n \geq N\)ならば,\(|a_n-\alpha|<\epsilon\)とできるので,\(k \geq N\)とすれば,\(|a_{n(k)}-\alpha|<\epsilon\)とできる.■
(2)(1)の対偶をとると,一つでも収束しない部分列があれば,元の数列は収束しません.
(3)逆に,元の数列が収束していなくても,ある部分列が収束することがあります.
$$例: a_n = (-1)^nは収束しないが(振動する),部分列\{a_{2n}\}は1に収束する.$$
そして,「有界な数列であれば,常に収束する部分列を持つ」というのが,ボルツァーノ・ワイエルシュトラスの定理の主張です.
証明
では,ボルツァーノ・ワイエルシュトラスの定理を証明します.
証明のポイントは,数列の有界性から区間縮小法を使う点です.
また,アルキメデスの原理も使います.
有界な単調増加数列の収束先は?アルキメデスの原理の証明(解析学 第I章 実数と連続4)
証明:
数列は有界なので,ある実数\(b,c\)が存在して,\(\forall n, a_n \in [b,c]\)とできる.
有界閉区間\(I_0 = [b_0,c_0]=[b,c]\)とする.
以後,単調減少となるように,有界閉区間\(I_n\)を次のように帰納的につくる.
\(I_n = [b_n,c_n]\)のとき,
\(b_n\)と\(c_n\)の中間点を\(d_n = \displaystyle \frac{b_n+c_n}{2}\)とし,
\([b_n,d_n],[d_n,c_n]\)のうち,\(a_n\)の項が無限個含む方を新たに\(I_{n+1}\)とする.
もし両方に無限個の項が含まれる場合は,\(I_{n+1}=[d_n,c_n]\)とする.
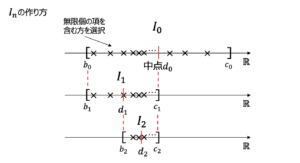
閉区間の作り方から,$$I_0 \supset I_1 \supset \cdots \supset I_n \supset I_{n+1} \supset \cdots$$
また,$$c_n-b_n=\displaystyle \frac{c_{n-1}-b_{n-1}}{2}$$$$=\displaystyle \frac{c_{n-2}-b_{n-2}}{2^2}$$$$=\cdots$$$$=\displaystyle \frac{c_0-b_0}{2^n}$$$$=\displaystyle \frac{c-b}{2^n}\longrightarrow 0 (n \to \infty)$$(∵アルキメデスの原理より)
したがって,区間縮小法より,$$\displaystyle \lim_{n \to \infty}b_n = \displaystyle \lim_{n \to \infty}c_n = \alpha \in \mathbb{R}.$$\(I_n\)の作り方から,任意の自然数\(n\)に対して,\(\exists m \in \mathbb{N} s.t. a_m \in I_n\)
よって,数列\(\left \{a_{n(k)}\right \}\)で,任意の自然数\(k\)に対して,\(a_{n(k)}\in I_k\)となる部分列\(\left \{a_{n(k)}\right \}\)が作れる.
このように作った部分列\(\left \{a_{n(k)}\right \}\)の項は,$$\forall k, b_k \leq a_{n(k)} \leq c_k$$である.
よって,はさみうちの原理より,$$\displaystyle \lim_{k \to \infty}a_{n(k)}=\alpha$$
よって,この部分列が収束することが示せた.
■
まとめ(実数の連続性公理)
Dedekindの切断に関する実数の連続性公理から議論をスタートして,収束の定義によって今まで分かったことを次でまとめておきます.


はじめまして。
分かりやすい解説ありがとうございます。
図等でイメージしやすく、学習させて戴いてます。
1点確認ですが、収束する部分列の例の(1)の証明ですが、kとNの不等号が逆ですかね?
satsubatsutaroさん
こんにちは。
コメントいただきありがとうございます。
これからも学んだ数学を分かりやすくお伝えしたいと思います。
ご指摘のとおり、不等号が逆になっておりました。
正しくはk≧Nでした。
ご指摘ありがとうございました。
yuyu