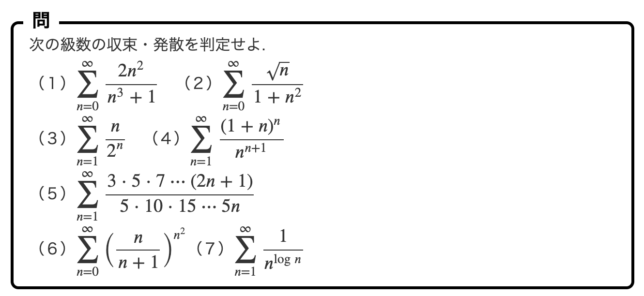
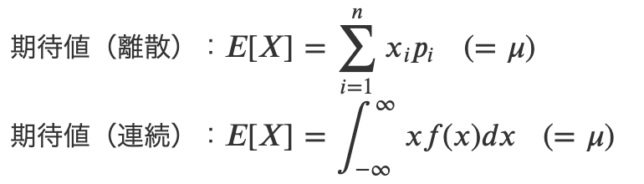本稿では級数の収束,発散についてまとめました.
Cauchyの収束条件からダランベールの収束判定法(ratio test)まで証明を行い,実際に例題を解いて使い方を解説します.
投稿者: yuyu
加藤文元「宇宙と宇宙をつなぐ数学」教養としての数学者の発想
IUT理論とはInter Universal Teichmüller理論=宇宙際(うちゅうさい)タイヒミュラー理論のことで,京都大学望月教授が2012年8月30日に発表し数学会に衝撃を与えている理論です.
加藤文元教授による著書「宇宙と宇宙をつなぐ数学 IUT理論の衝撃」では,IUT理論の雰囲気が分かりやすく紹介がされています.
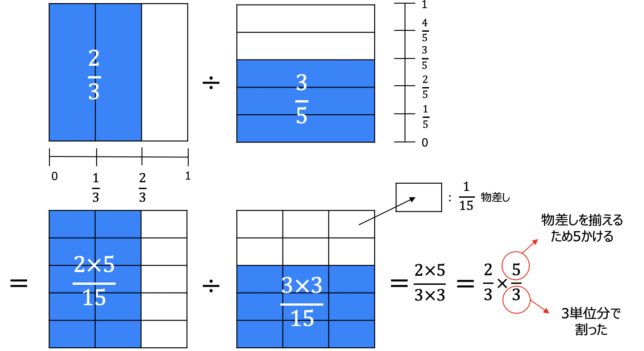
何で分数の割り算は逆数をかけるの?理由を説明できますか?
もし子供に「何で分数の割り算は逆数をかけるの?」と聞かれたら,何と答えますか?
小学校で分数の割り算の仕方は習いましたが,何でそうなのかと改めて考えると結構難しいものです.
今回は割り算に関して,その本質に迫り,上記質問の回答を考えたいと思います.
子供への数学教育としてどうぞ.
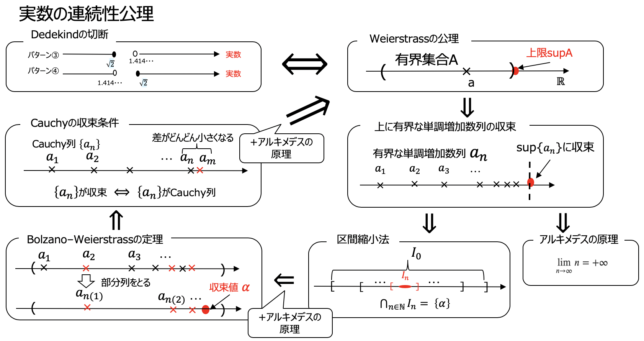
6つの同値な「実数の連続性公理」まとめ(解析学 第I章 実数と連続9)
これまで実数の連続性を公理とし,数列の極限について定義,それから導かれる様々な命題,定理を証明してきました.
その結果分かった実数の連続性公理と同値な条件(Bolzano–Weierstrass,Cauhy列の収束+アルキメデスの原理etc)
をまとめたいと思います.
どれを公理としてもよく,自分にあったものを議論の出発点としてよいのです.
コーシーの収束条件から実数の連続性を証明(解析学 第I章 実数と連続8)
我々は今,実数の連続性を公理とし,数列の極限について定義,様々な極限操作を論理的に厳密に扱えるようになりました.
そして,数列の収束を判定するCauchyの収束判定条件を証明しました.
実は,アルキメデスの原理を加えれば,これははじめに仮定した「実数の連続性公理」と同値なのです.
今回はこれを証明します.
サンプル平均の期待値,分散,不偏推定量まとめ(統計検定準1級対策2)
統計検定準1級に合格するには,短い時間内に大量の処理をする必要があります.
それには過去問を素早く解く練習が適しています.
問題を解く際に覚えておくべきサンプル平均の期待値,分散,不偏推定量についてまとめました.
これらは,標準化や中心極限定理でも利用する重要な性質です.
期待値,分散,共分散,相関係数,変動係数まとめ(統計検定準1級対策1)
統計検定準1級に合格するには,短い時間内に大量の処理をする必要があります.
それには過去問を素早く解く練習が適しています.
問題を解く際に覚えておくべき期待値,分散,共分散,相関係数,変動係数の基本公式をまとめました.
合格にはまずはこれらを公式として暗記しすぐに計算できるようにします.
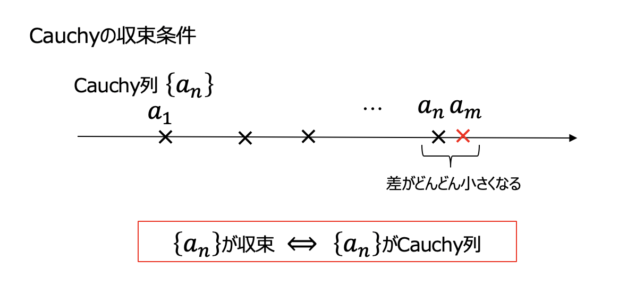
コーシーの収束条件(解析学 第I章 実数と連続7)
数列が収束する条件があると便利です.極限値は分からなくても,数列がCauchy(コーシー)列であれば,収束することが分かります.今後も使う非常に有用な定理です.今回はCauchy列が収束することを分かりやすく証明します.
ボルツァーノ・ワイエルシュトラスの定理の証明(解析学 第I章 実数と連続6)
同じ誕生日の人がいる確率〜誕生日パラドックス〜
昔,学校のクラスで同じ誕生日の人はいたでしょうか.
いたらその人と運命を感じるものです.
その運命,どのくらいの確率なのか計算してみると,
直感に反する意外な事実が分かります.
誕生日の話のネタとしてどうぞ.